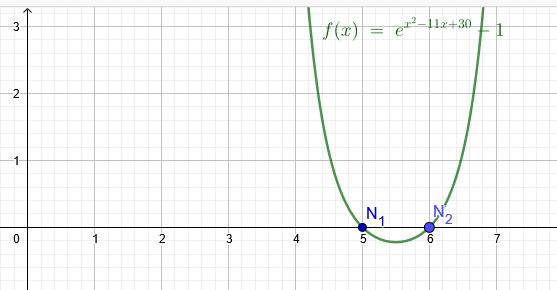
\(f(x)=e^{x^2−11\cdot x+30}−1\)
\(e^{x^2−11⋅x+30}−1=0\)
\(e^{x^2−11\cdot x+30}=1\) Nun gilt \(e^{0}=1\)
\(e^{x^2−11\cdot x+30}=e^{0}\)
\(x^2−11\cdot x+30=0\)
\(x^2−11\cdot x=-30\) quadratische Ergänzung:
\(x^2−11\cdot x+(\frac{11}{2})^2=-30+(\frac{11}{2})^2\) 2.Binom:
\((x−\frac{11}{2})^2=-30+5,5^2=0,25|±\sqrt{~~}\)
1.)
\(x−5,5=0,5\)
\(x_1=6\)
2.)
\(x−5,5=-0,5\)
\(x_2=5\)
L={5,6}