Aufgabe:
Ich verstehe die Definition der Normalform (lineare Algebra) im Skript nicht
Problem/Ansatz:
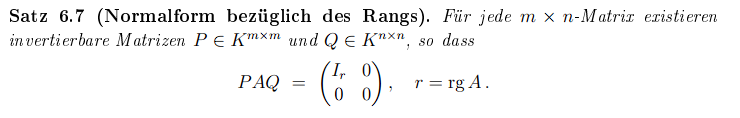
Text erkannt:
Satz 6.7 (Normalform bezüglich des Rangs). Für jede \( m \times n \)-Matrix existieren invertierbare Matrizen \( P \in K^{m \times m} \) und \( Q \in K^{n \times n} \), so dass
\( P A Q=\left(\begin{array}{cc} I_{r} & 0 \\ 0 & 0 \end{array}\right), \quad r=\operatorname{rg} A \)
Ich verstehe nicht, was davon jetzt die Normalform ist und was dieses Ir heißt. Ich weiss, dass Ir eigentlich für die r*r Identitätsmatrix steht aber wie kommt man jetzt auf die und wie kann diese ein Eintrag in einer Matrix sein?