Hi, kann mir jemand dabei helfen, wie ich diese Aufgaben lösen kann?: Die Funktionsgleichungen sind gesucht außer bei 5.)
Die Zeichen || soll für parallel stehen
Text erkannt:
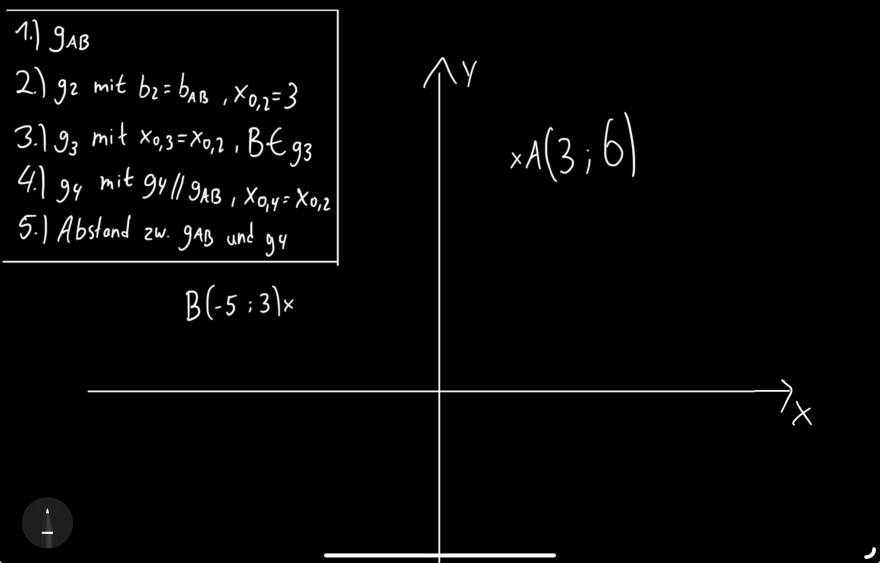
1.) \( g_{A B} \)
2) \( g_{2} \) mit \( b_{2}=b_{A B}, x_{0,2}=3 \)
3.) \( g_{3} \) mit \( x_{0,3}=x_{0,2}, B \in g_{3} \)
4.) \( g_{4} \) mit \( g_{4} / / g_{A B}, x_{0,4}=x_{0,2} \)
5.) Abstand \( zwischen \). gaB und g4
\( \)