Hinweis: Wie viele Lösungen besitzt die Gleichung f_{1}(z)=w für ein beliebiges, aber festes w ∈ ℂ?

Question

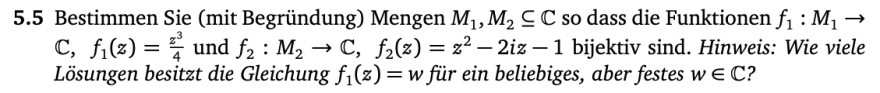
Text erkannt:

5.5 Bestimmen Sie (mit Begründung) Mengen \( M_{1}, M_{2} \subseteq \mathbb{C} \) so dass die Funktionen \( f_{1}: M_{1} \rightarrow \) \( \mathbb{C}, f_{1}(z)=\frac{z^{3}}{4} \) und \( f_{2}: M_{2} \rightarrow \mathbb{C}, f_{2}(z)=z^{2}-2 i z-1 \) bijektiv sind. Hinweis: Wie viele Lösungen besitzt die Gleichung \( f_{1}(z)=w \) für ein beliebiges, aber festes \( w \in \mathbb{C} \) ?

Problem/Ansatz:

Wie muss ich hier vorgehen?

Answer 1

hallo

du hast doch den Hinweis. dann sieh nach ob es zu einer Lösung mehr als ein Urbild gibt.

Gruß lul