erste Ableitung berghang gleichung bestimmen

Question

Aufgabe:

Ein Berghang lässt sich im Intervall I = (1;2,5) durch die Funktion b (x) = x2-2x +2 beschreiben. Am Punkt E (2 / B(2)) soll ein senkrecht zum Hang verlaufender Besucherstollen gebohrt werden.

Veranschaulichen Sie das Problem mittels Zeichnung.

Ermittle den Anstiegswinkel des Berghangs am Eingang E des Stollens.

Stellen Sie eine Gleichung für den geradlinigen Stollen auf.
Untersuchen Sie die gegebene Funktion auf Wendepunkte!

Problem/Ansatz:

Answer 1

Gesucht ist die Normale im angegebenen Punkt. Dies geht mit Hilfe der Tangente, da diese senkrecht zur Kurve ist.

Eine Skizze schaffst du hoffentlich alleine. Den Winkel erhält man über \(m=\tan(\alpha)\)

Wendepunkte findet man über die zweite Ableitung.

Answer 2

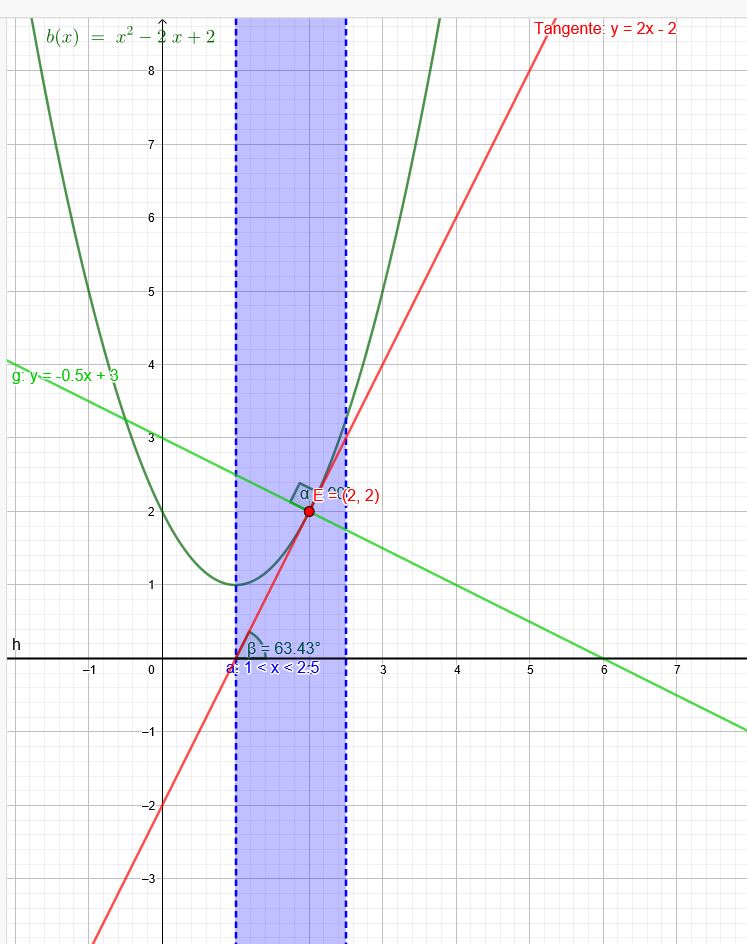
Ein Berghang lässt sich im Intervall \(I = (1;2,5)\) durch die Funktion \(b (x)=x^2-2x +2\) beschreiben. Am Punkt \(E (2 | 2)\) soll ein senkrecht zum Hang verlaufender Besucherstollen gebohrt werden.

\(b ´(x)=2x-2\)

\(b ´(2)=2*2-2=\red{2}\)

Tangente:

\( \frac{y-2}{x-2}=\red{2} \)

\( y  =\red{2}*(x-2) +2=\red{2}x-2\)    Anstiegswinkel des Berghangs : \( tan^{-1}(\red{2})=63,43° \)

Der Besucherstollen erscheint als Normale zur Tangente:

\( \frac{y-2}{x-2}=\red{-}\frac{1}{\red{2}} \)

\( y=\red{-}\frac{1}{\red{2}} x+3\)

Eine quadratische Parabel hat keinen Wendepunkt. Eventuell ist \(b(x)=x^2-2x +2\) nicht die richtige Funktion.

Comments

Kann es sein, dass die Funktion \( f(x)=x^3-2x^2+2\) lautet ?