Aufgabe:
Ermitteln Sie den idealen Standort der Talstation eines Sessellifts und untersuchen Sie dessen Auslastung nach einem Jahr.
Problem/Ansatz:
Ich verstehe nicht, wie man die Aufgaben löst, deswegen wollte ich hier mal nachfragen. Ich würde gerne den Rechenweg wissen, wie man zu welchem Ergebnis kommt und was dann zum Schluss rauskommt.Ich würde mich über jede Hilfe freuen und ich bedanke mich schon im voraus.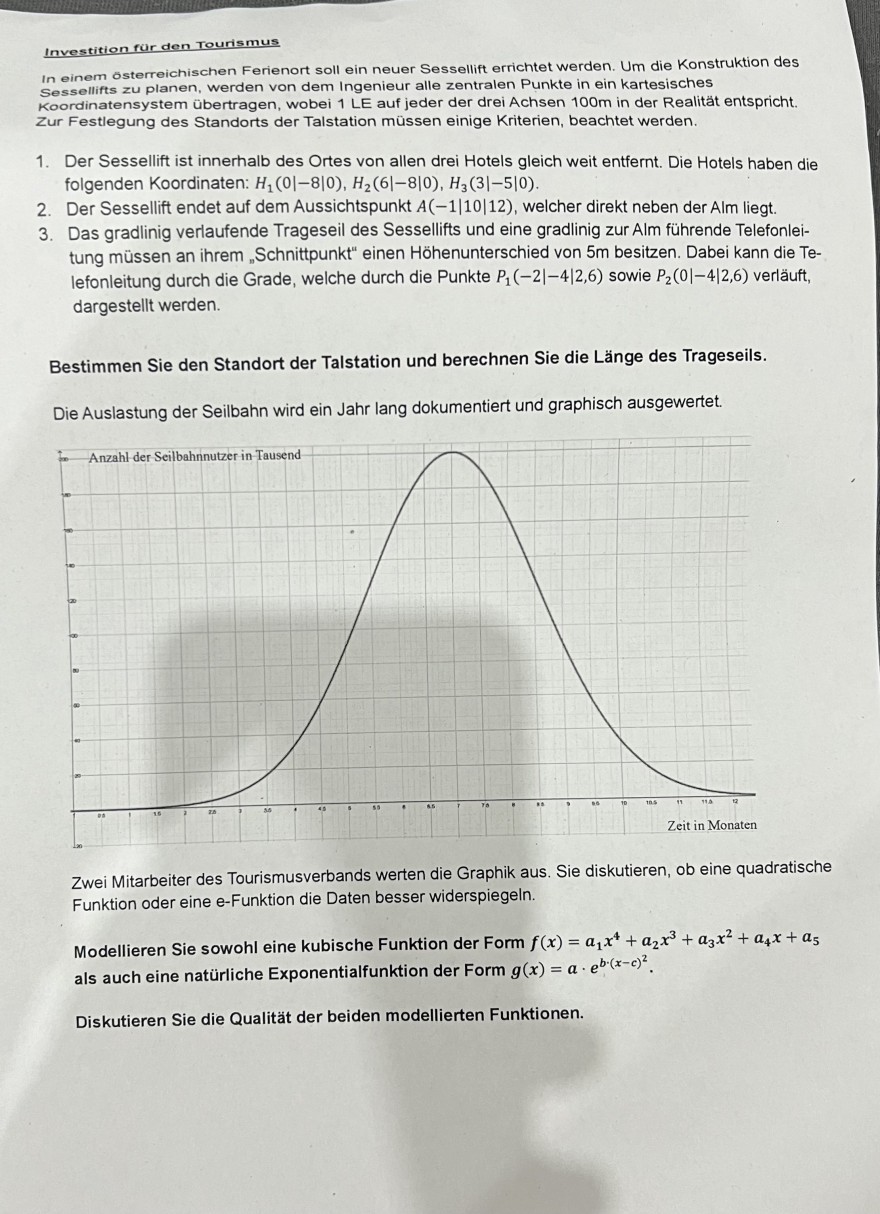
Text erkannt:
In einem österreichischen Ferienort soll ein neuer Sessellift errichtet werden. Um die Konstruktion des Sessellifts zu planen, werden von dem Ingenieur alle zentralen Punkte in ein kartesisches Koordinatensystem übertragen, wobei 1 LE auf jeder der drei Achsen \( 100 \mathrm{~m} \) in der Realität entspricht. Zur Festlegung des Standorts der Talstation müssen einige Kriterien, beachtet werden.
1. Der Sessellift ist innerhalb des Ortes von allen drei Hotels gleich weit entfernt. Die Hotels haben die folgenden Koordinaten: \( H_{1}(0|-8| 0), H_{2}(6|-8| 0), H_{3}(3|-5| 0) \).
2. Der Sessellift endet auf dem Aussichtspunkt \( A(-1|10| 12) \), welcher direkt neben der Alm liegt.
3. Das gradlinig verlaufende Trageseil des Sessellifts und eine gradlinig zur Alm führende Telefonleitung müssen an ihrem "Schnittpunkt" einen Höhenunterschied von \( 5 \mathrm{~m} \) besitzen. Dabei kann die Telefonleitung durch die Grade, welche durch die Punkte \( P_{1}(-2|-4| 2,6) \) sowie \( P_{2}(0|-4| 2,6) \) verläuft, dargestellt werden.
Bestimmen Sie den Standort der Talstation und berechnen Sie die Länge des Trageseils.
Die Auslastung der Seilbahn wird ein Jahr lang dokumentiert und graphisch ausgewertet.
Zwei Mitarbeiter des Tourismusverbands werten die Graphik aus. Sie diskutieren, ob eine quadratische Funktion oder eine e-Funktion die Daten besser widerspiegeln.
Modellieren Sie sowohl eine kubische Funktion der Form \( f(x)=a_{1} x^{4}+a_{2} x^{3}+a_{3} x^{2}+a_{4} x+a_{5} \) als auch eine natürliche Exponentialfunktion der Form \( g(x)=a \cdot e^{b \cdot(x-c)^{2}} \).
Diskutieren Sie die Qualität der beiden modellierten Funktionen.