Wie groß ist der Inhalt der abgebildeten Fläche A?

Question

Aufgabe:

17. Flächenberechnung mit drei Funktionen

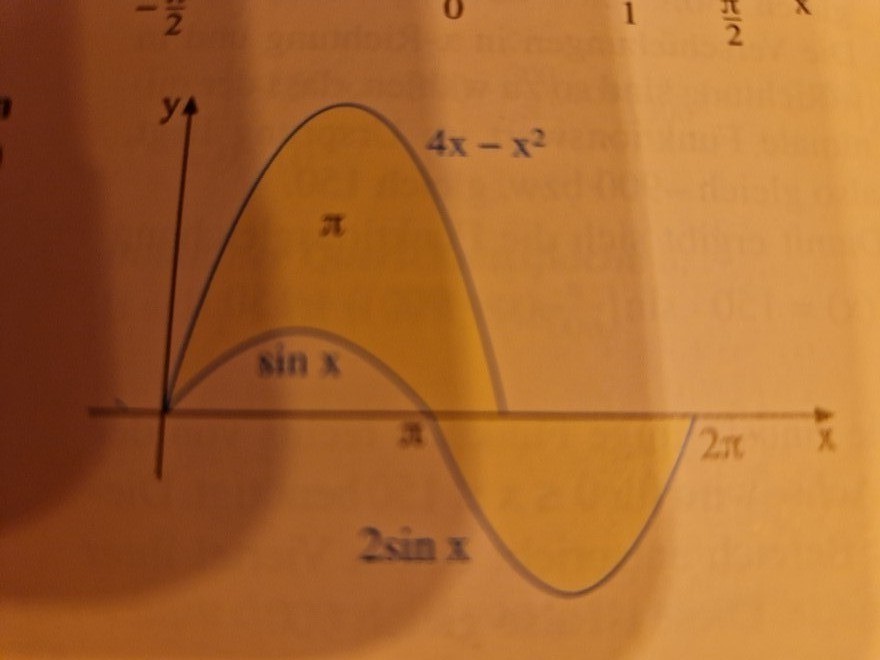
Wie groß ist der Inhalt der abgebildeten Fläche A?

A wird von den Graphen der drei Funk- tionen f(x) = sin x, g(x) = 2sin x, h(x) = 4x - x ^ 2 sowie von der x-Achse begrenzt.

Problem/Ansatz:

Wie soll ich das berechnen?

Answer 1

\(A_1= \int\limits_{0}^{4}((4x-x^2)dx \)

davon abziehen:

\(A_3= \int\limits_{0}^{π}sin(x)dx \)

dazu kommt

\(A_2= \int\limits_{π}^{2π}2sin(x)dx \)  !!! aufpassen

Answer 2

Hallo,

Wie soll ich das berechnen?

teile den Abschnitt von 0 bis \(2\pi\) in drei Bereiche und rechne jeden Bereich für sich.

Die Fläche hat die Größe \(38/3\)FE.

Gruß Werner

Comments

.. oder Du rechnest es im Kopf aus!

Die Fläche unter der Parabel ist \((2/3) \cdot 4 \cdot 4\), die unter der ersten Sinusschwinge ist 2 und unter der zweiten ist das Doppelte also 4. Macht$$F = \frac{32}{3} - 2 + 4 = \frac{38}{3}$$