Bestimmen Sie a > 0 so, dass die von den Graphen f und g eingeschlossene Fläche den angegebenen Inhalt A hat.

Question

Aufgabe:

Bestimmen Sie a>0 so, dass die von den Graphen f und g eingeschlossene Fläche den angegebenen Inhalt A hat.

f(x) = x^2 + 1

g(x) = (a^2+1) • x^2

A = 4/3

Problem/Ansatz:

Ansatz: f(x)=g(x)

Wie muss ich jetzt weiter rechnen?

Answer 1

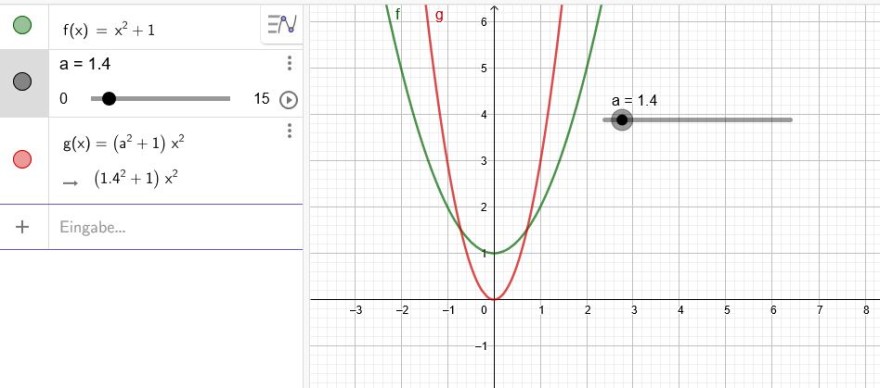
\(f(x)= x^2+1\)     \(g(x)= (a^2+1)•x^2\)        \(A= \frac{4}{3}\)
Schnittpunkte:
\(x^2+1= (a^2+1)•x^2 \)  →  \(x^2+1=a^2•x^2 +x^2\)    →  \(a^2•x^2 =1\)→  \(x^2 =\frac{1}{a^2}\)→

\(x_1 =-\frac{1}{a}\)   \(x_2 =\frac{1}{a}\) Wegen der Symmetrie kannst du so weiterrechnen;

\(\frac{2}{3}=\int\limits_{0}^{\frac{1}{a}}(f(x)-g(x))dx\)

\((f(x)-g(x))=x^2-\frac{1}{a^2}\)

Schau mal die Kommentare an. Da ist es nun richtig.

Comments

Die letzte Zeile ist falsch.

---

Danke dir, da habe ich wohl zu schnell gerechnet:

\(f(x)=x^2+1\)       \(g(x)=(a^2+1)*x^2\)

\(d(x)=f(x)-g(x)=x^2+1-[(a^2+1)*x^2]\)

\(d(x)=x^2+1-[a^2*x^2+x^2]\)

\(d(x)=x^2+1-a^2*x^2-x^2\)

 \(d(x)=1-a^2*x^2\)

Answer 2

Die Schnittpunkte sind die Grenzen des Integrals.

Dann rechnest du

\( \int\limits_{a}^{b}f(x)-g(x)dx \)=4/3

dann nach a umstellen.

Comments

Die untere Grenze mit a zu bezeichnen, ist hier nicht ratsam.

---

... auf die Klammer um die Summe im Integranden zu verzichten, ist auch unschön.

---

... auf die Klammer um die Summe im Integranden zu verzichten, ist auch unschön.

Das sehe ich auch so.

Answer 3

x^2+1 = a^2 x^2+x^2

a^2 x^2 = 1

x^2 = 1/a^2

x= ±1/a

f(x)-g(x)

x^2+1-a^2 x^2-x^2 = 1-a^2 x^2

Integriere 2*(1-a^2*x^2) von 0 bis 1/a und setze das Integral gleich 4/3

Comments

In der ersten Zeile muss a quadriert weren.

---

Danke, das Quadrat ging verloren.

Answer 4

f(x) = x^2 + 1

g(x) = (a^2 + 1)·x^2

d(x) = f(x) - g(x) = x^2 + 1 - (a^2 + 1)·x^2 = 1 - a^2·x^2

D(x) = x - 1/3·a^2·x^3

d(x) = 1 - a^2·x^2 = 0 --> x = ± 1/a

A = 2·∫ (0 bis 1/a) d(x) dx = 2·D(1/a) = 2·(1/a - 1/3·a^2·(1/a)^3) = 4/(3·a) = 4/3

Damit muss a also offensichtlich den Wert 1 annehmen.