
Text erkannt:
\( 00: 47 \)
2. Lagebeziehungen
42. Untersuchen Sie, welche gegenseitige Lage die Ebenen \( \mathrm{E}_{1} \) und \( \mathrm{E}_{2} \) einnehmen.
a) \( E_{1}: 2 x+y+z=6 \quad E_{2}: \vec{x}=\left(\begin{array}{r}-2 \\ -2 \\ 3\end{array}\right)+r\left(\begin{array}{l}1 \\ 1 \\ 0\end{array}\right)+s\left(\begin{array}{r}2 \\ 0 \\ -3\end{array}\right) \)
b) \( E_{1}: x-y+z=2 \quad E_{2}: \vec{x}=\left(\begin{array}{r}7 \\ 1 \\ -4\end{array}\right)+r\left(\begin{array}{l}1 \\ 1 \\ 0\end{array}\right)+s\left(\begin{array}{r}1 \\ 0 \\ -1\end{array}\right) \)
c) \( E_{1}: 2 x-5 y-5 z=8 \quad E_{2}: \vec{x}=\left(\begin{array}{r}0 \\ -1 \\ -1\end{array}\right)+r\left(\begin{array}{l}5 \\ 1 \\ 1\end{array}\right)+s\left(\begin{array}{l}5 \\ 2 \\ 0\end{array}\right) \)
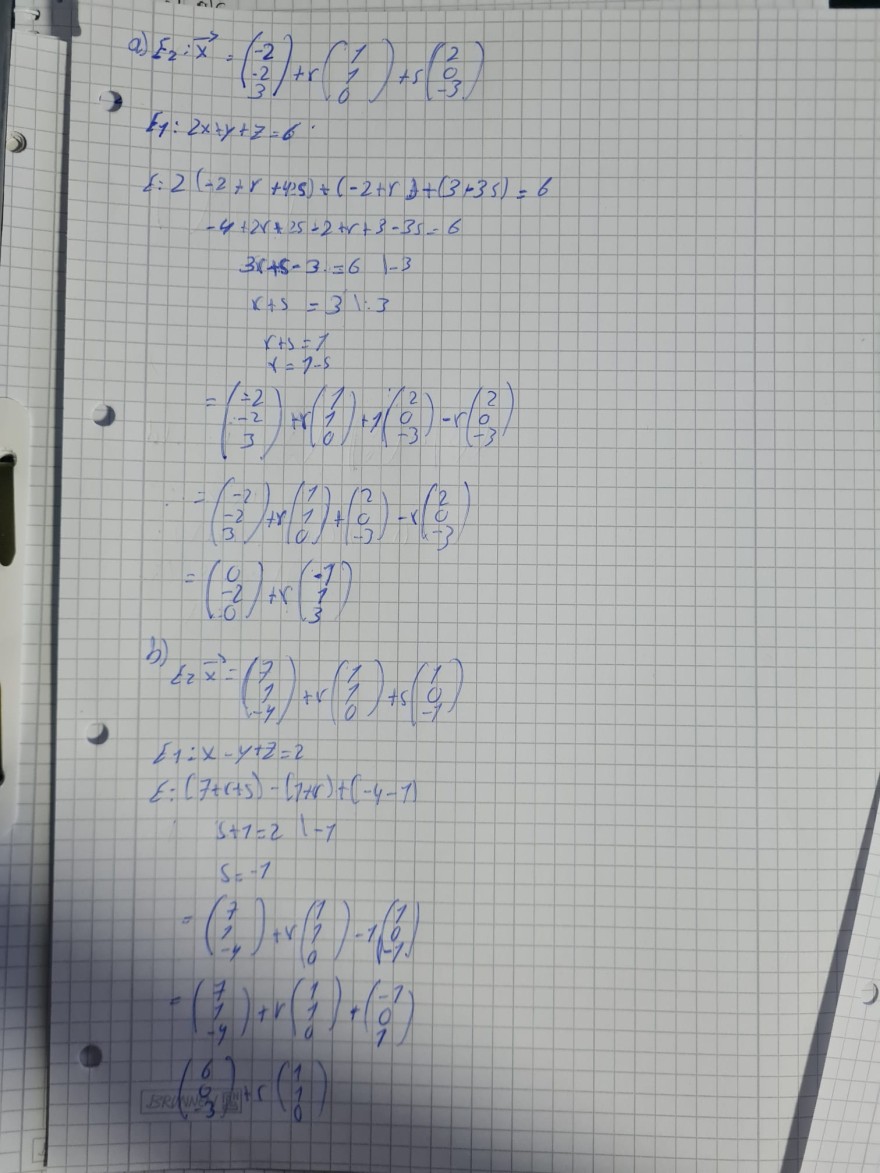
Text erkannt:
\( \begin{array}{l} \text { a) } E_{2}: \vec{x}=\left(\begin{array}{c} -2 \\ -2 \\ 3 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)+s\left(\begin{array}{c} 2 \\ 0 \\ -3 \end{array}\right) \\ E_{1}: 2 x+y+z=6 \\ \{: 2(-2+r+4 s)+(-2+r)+(3+3 s)=6 \\ -4+2 r+2 s-2+r+3-3 s=6 \\ 3 r+s-3 \cdot=61-3 \\ x+s=31: 3 \\ r+s=1 \\ r=1-s \\ =\left(\begin{array}{c} -2 \\ -2 \\ 3 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)+1\left(\begin{array}{c} 2 \\ 0 \\ -3 \end{array}\right)-r\left(\begin{array}{c} 2 \\ 0 \\ -3 \end{array}\right) \\ =\left(\begin{array}{c} -2 \\ -2 \\ 3 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)+\left(\begin{array}{c} 2 \\ 0 \\ -3 \end{array}\right)-r\left(\begin{array}{c} 2 \\ 0 \\ -3 \end{array}\right) \\ =\left(\begin{array}{c} 0 \\ -2 \\ 0 \end{array}\right)+r\left(\begin{array}{c} -1 \\ 1 \\ 3 \end{array}\right) \end{array} \)
b)
\( \operatorname{tz} \vec{x}^{3}=\left(\begin{array}{c} 7 \\ 1 \\ -4 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)+5\left(\begin{array}{c} 1 \\ 0 \\ -1 \end{array}\right) \)
\( \begin{array}{l} E_{1}: x-y+z=2 \\ E:(7+r+5)-(1+r)+(-4-1) \\ s+1=2 \quad 1-1 \\ 5=-1 \\ =\left(\begin{array}{c} 7 \\ 1 \\ -4 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)-1\left(\begin{array}{c} 1 \\ -1 \\ -1 \end{array}\right) \\ =\left(\begin{array}{c} 7 \\ 1 \\ -4 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right)+\left(\begin{array}{c} -1 \\ 0 \\ 1 \end{array}\right) \\ \left(\begin{array}{c} 6 \\ 0 \\ -3 \end{array}\right)+r\left(\begin{array}{l} 1 \\ 1 \\ 0 \end{array}\right) \end{array} \)

Text erkannt:
c) \( \varepsilon_{2}: \vec{x}=\left(\begin{array}{c}0 \\ -1 \\ -1\end{array}\right)+r\left(\begin{array}{l}5 \\ 1\end{array}\right)+s\left(\begin{array}{l}5 \\ 2 \\ 0\end{array}\right) \)
\( \begin{array}{c} E_{1}=2 x-5 y-5 z=8 \\ \text { E: } 2(0+5 r+55)-5(-7+r+25)-5(-1+r)=8 \\ 10=8 \end{array} \)
nicht identarch
Kann mir jemand sagen, ob meine Lösungen richtig sind?
Aufgabe:
…
Problem/Ansatz: