Bestimmen Sie den Abstand zwischen dem Auto rot ▭ und der Wand blau — .

Question

Aufgabe:

 

Bestimmen Sie den Abstand zwischen blau und rot.


Gesucht: Projektionspunkt P und den Abstand


Problem/Ansatz:

Kann mir da jemand helfen, ich weiß nicht wie das funktioniert.

Answer 1

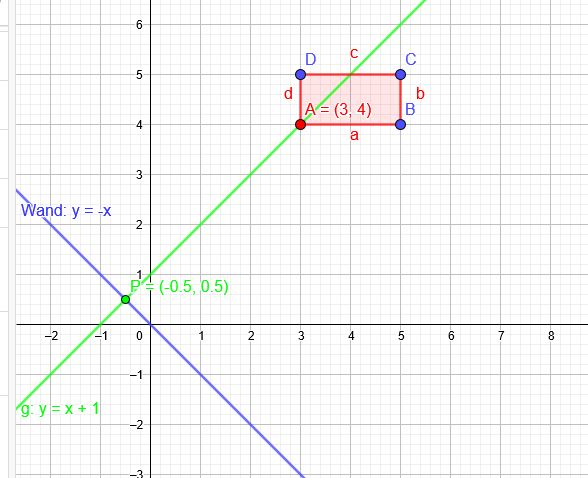
Die Wand hat die Geradengleichung \(g_1(x)=-x\).

Die Abstandsgerade steht senkrecht auf dieser und hat die Steigung \(m_N=1\). Sie muss durch \(A(3|4)\) gehen.

\( \frac{y-4}{x-3} =1\)  →\( g(x)=x+1\)

Projektionspunkt :

\(-x=x+1\) → \(x=-\frac{1}{2}\)        \(g(-\frac{1}{2})=-\frac{1}{2}+1=\frac{1}{2}\)

\(P(-\frac{1}{2}|\frac{1}{2})\)

Abstand:

\(a= \sqrt{(3+0,5)^2+(4-0,5)^2}≈4,949 \)