Aufgabe
Ich verstehe den Unformungsschritt nicht. Das F ist unabhängig von t deswegen wird es vor das Integrsl gezogen. Der zeitlich konstante Fluss (großes Phi) eigentlich auch. Er wird ja auch mit nach vorne gezogen. Aber trotzdem auch noch mit ausgewertet. Also zuerst steht er da nur einmal (erste Zeile) 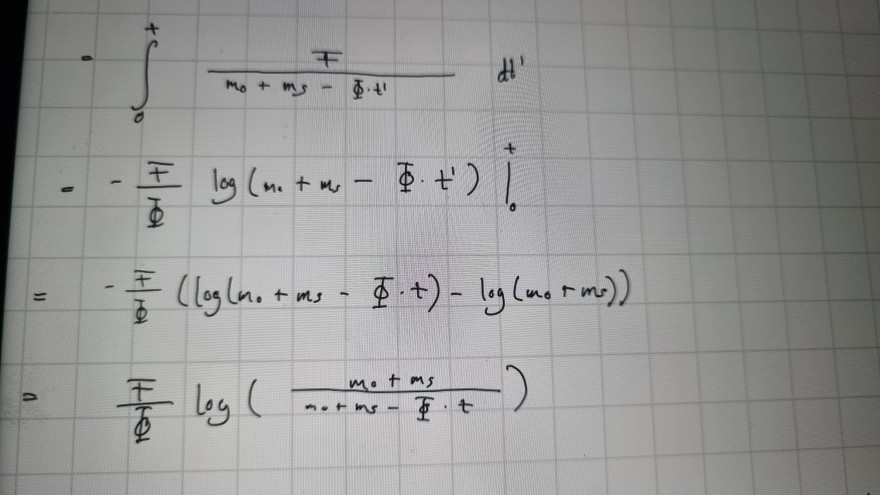
Text erkannt:
\( \begin{array}{l}=\int \limits_{0}^{+} \frac{\mp}{m_{0}+m_{s}-\Phi \cdot t^{\prime}} d t^{\prime} \\ =-\left.\frac{F}{\Phi} \log \left(m_{0}+m_{0}-\Phi \cdot t^{\prime}\right)\right|_{0} ^{t} \\ =-\frac{F}{\Phi}\left(\log \left(m_{0}+m_{s}-\Phi \cdot t\right)-\log \left(m_{0}+m_{s}\right)\right) \\ =\frac{F}{\Phi} \log \left(\frac{m_{0}+m_{s}}{m_{0}+m_{s}-\Phi \cdot t}\right)\end{array} \)
und dann auf einmal zweimal.
Wieso ist das so?