Text erkannt:
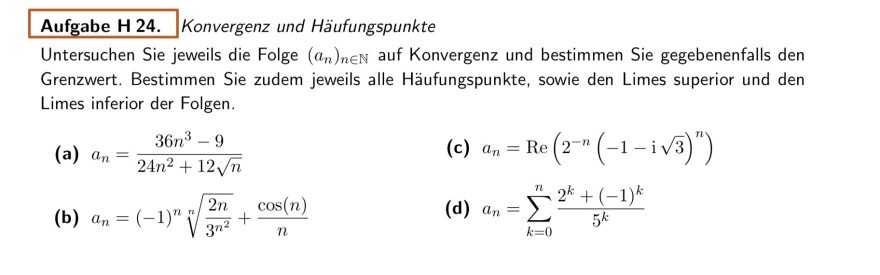
Aufgabe H 24. Konvergenz und Häufungspunkte
Untersuchen Sie jeweils die Folge \( \left(a_{n}\right)_{n \in \mathbb{N}} \) auf Konvergenz und bestimmen Sie gegebenenfalls den Grenzwert. Bestimmen Sie zudem jeweils alle Häufungspunkte, sowie den Limes superior und den Limes inferior der Folgen.
(a) \( a_{n}=\frac{36 n^{3}-9}{24 n^{2}+12 \sqrt{n}} \)
(c) \( a_{n}=\operatorname{Re}\left(2^{-n}(-1-\mathrm{i} \sqrt{3})^{n}\right) \)
(b) \( a_{n}=(-1)^{n} \sqrt[n]{\frac{2 n}{3^{n^{2}}}}+\frac{\cos (n)}{n} \)
(d) \( a_{n}=\sum \limits_{k=0}^{n} \frac{2^{k}+(-1)^{k}}{5^{k}} \)
Hallo, ich möchte gerne diese Aufgabe bearbeiten, doch weiß leider nicht, wie ich diese lösen kann. Sollte ich hier mit dem Epsilon-Kriterium vorgehen?
LG