Aufgabe:
Textaufgabe Integralrechnung
Problem/Ansatz:
Kann mir jemand bei dieser Aufgabe hilfen oder lösung nennen, komme garnicht weiter
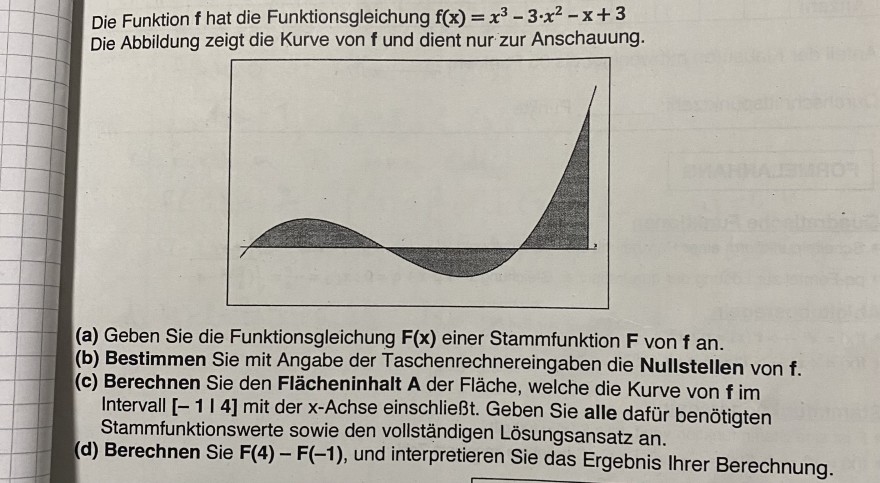
Text erkannt:
Die Funktion \( \mathrm{f} \) hat die Funktionsgleichung \( \mathrm{f}(\mathrm{x})=x^{3}-3 \cdot x^{2}-\mathrm{x}+3 \) Die Abbildung zeigt die Kurve von \( f \) und dient nur zur Anschauung.
(a) Geben Sie die Funktionsgleichung \( F(x) \) einer Stammfunktion \( F \) von \( \mathbf{f} \) an.
(b) Bestimmen Sie mit Angabe der Taschenrechnereingaben die Nullstellen von \( f \).
(c) Berechnen Sie den Flächeninhalt A der Fläche, welche die Kurve von \( f \) im Intervall [-1 1 4] mit der \( x \)-Achse einschließt. Geben Sie alle dafür benötigten Stammfunktionswerte sowie den vollständigen Lösungsansatz an.
(d) Berechnen Sie \( \mathbf{F}(\mathbf{4})-\mathbf{F}(-\mathbf{1}) \), und interpretieren Sie das Ergebnis Ihrer Berechnung.
