Text erkannt:
15:00 Dio, 28, Nov。 \( \mathbf{E} \mathbf{G} \).
순. \( 66 \% \)
Titel
广
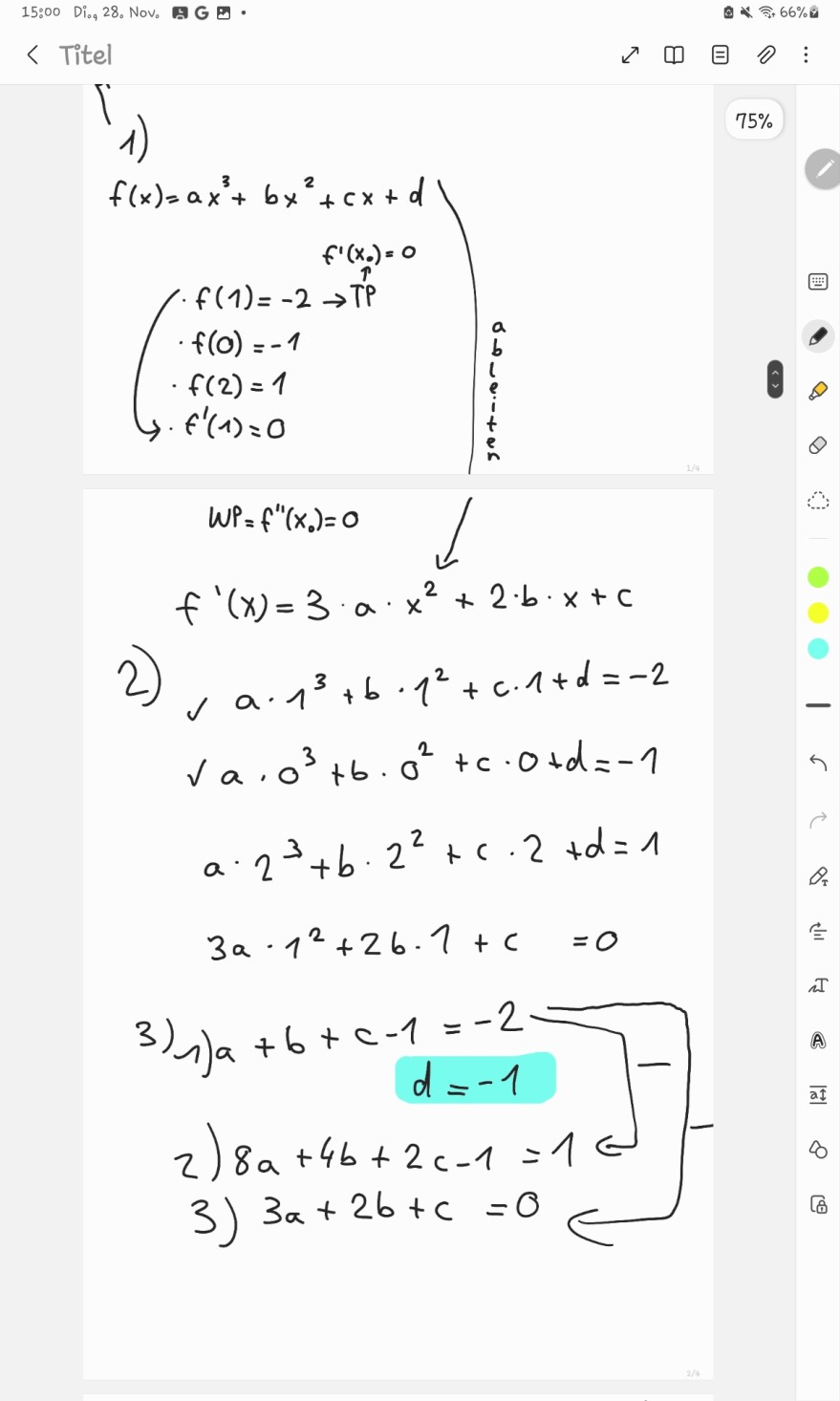
1)
\( 75 \% \)
\( \begin{array}{l} f(x)=a x^{3}+b x^{2}+c x+d \\ f^{\prime}\left(x_{0}\right)=0 \\ f(1)=-2 \rightarrow T^{\uparrow} p \\ f(0)=-1 \\ \text { - } f(2)=1 \\ f^{\prime}(1)=0 \\ W P=f^{\prime \prime}\left(x_{0}\right)=0 \\ f^{\prime}(x)=3 \cdot a \cdot x^{2}+2 \cdot b \cdot x+c \\ \end{array} \)
\( a \)
\( b \)
\( b \)
\( e \)
\( i \)
\( b \)
\( e \)
2)
\( \begin{array}{l} \checkmark a \cdot 1^{3}+b \cdot 1^{2}+c \cdot 1+d=-2 \\ \checkmark a \cdot 0^{3}+b \cdot 0^{2}+c \cdot 0+d=-1 \\ a \cdot 2^{3}+b \cdot 2^{2}+c \cdot 2+d=1 \\ 3 a \cdot 1^{2}+2 b \cdot 1+c=0 \end{array} \)
3)
\( \left.\begin{array}{rl} 1) a+b+c-1 & =-2 \\ d & =-1 \\ \text { 2) } 8 a+4 b+2 c-1 & =1 \\ \text { 3) } 3 a+2 b+c=0 \end{array}\right]- \)
Text erkannt:
15:00 Dio, 28, Novo D \( \mathbf{E} \mathbf{G} \).
ด《๐ \( 67 \% \)
Titel
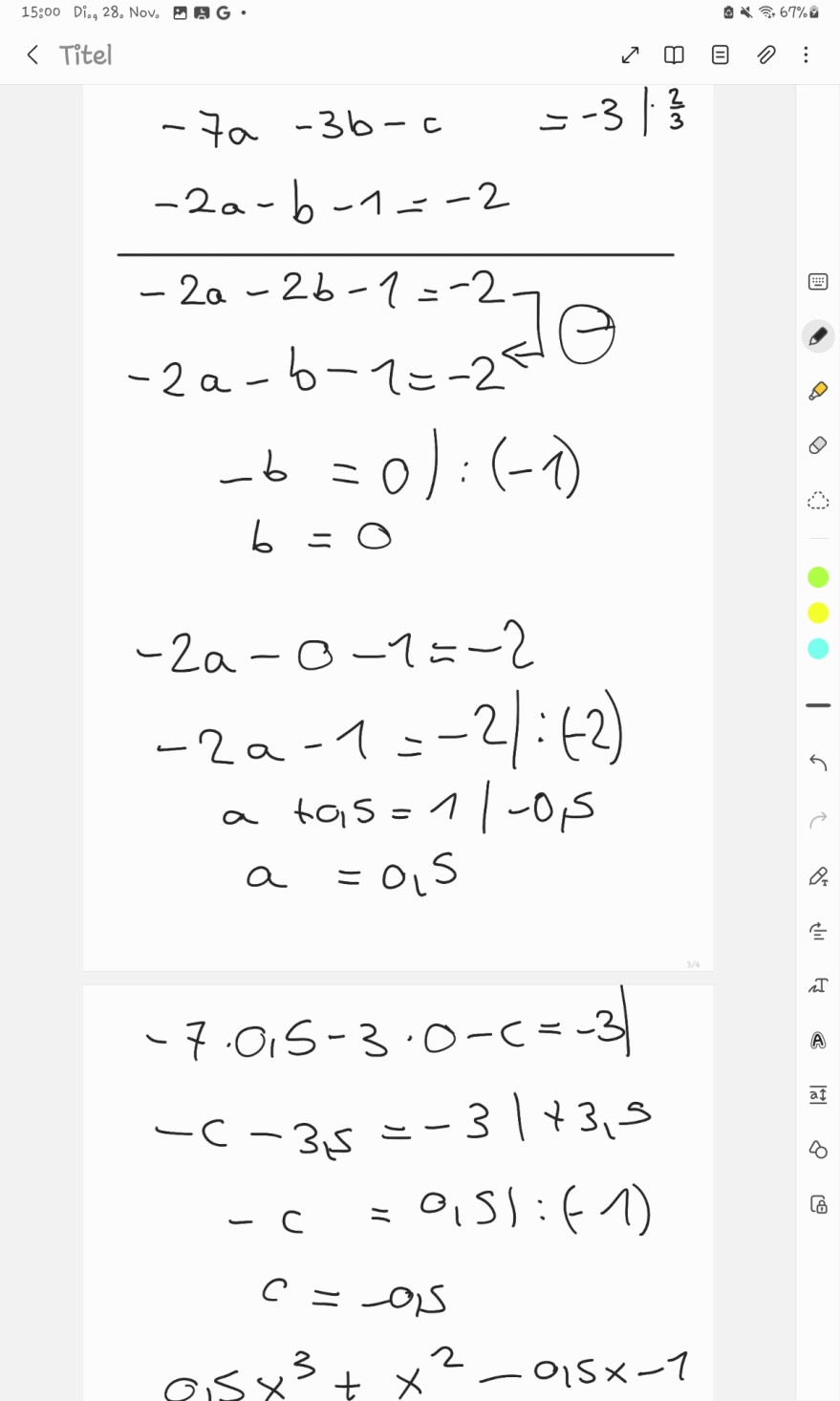
\( -7 a-3 b-c=-3 \mid \frac{2}{3} \)
\( \left.\begin{array}{l} -2 a-b-1=-2 \\ -2 a-2 b-1=-2 \\ -2 a-b-1=-2 \end{array}\right] \Theta \)
\( \begin{array}{c} -b=0):(-1) \\ b=0 \end{array} \)
\( \begin{array}{c} -2 a-0-1=-2 \\ -2 a-1=-2 \mid:(-2) \\ a+0,5=1 \mid-0,5 \\ a=0,5 \end{array} \)
\( \begin{array}{c} -7 \cdot 0,5-3 \cdot 0-c=-3 \mid \\ -c-3,5=-3 \mid+3,5 \\ -c=0,51:(-1) \\ c=-0,5 \end{array} \)
\( 0,5 x^{3}+x^{2}-0,5 x-1 \)

Text erkannt:
15:00 Dioq 28. Novo D \( \mathbf{0} \).
Titel
\( \begin{array}{c} b=0 \\ -2 a-0-1=-2 \\ -2 a-1=-2 \mid:(-2) \\ a+0,5=1 \mid-0,5 \\ a=0,5 \end{array} \)
\( \begin{array}{c} -7 \cdot 0,5-3 \cdot 0-c=-3 \mid \\ -c-3,5=-3 \mid+3,5 \\ -c=0,51:(-1) \\ c=-0,5 \\ 0,5 x^{3}+x^{2}-0,5 x-1 \end{array} \)
ich habe es nach diesem Verfahren gemacht, es sollte aber eigentlich "x^3-x^2-x-1" rauskommen. Ich habe den Taschenrechner Casio fx-CG 20 und bin auf Menu, Gleichungen, Polynomgleichung, Grad 3 gegangen. Dann war da eine Tabelle, wo oben a,b,c und d stand und ich musste für jede Variable einen Koefffizienten oder so eingeben. Ich wusste nicht was ich da eingeben soll und wenn ich da überhaupt etwas angebe, wird mir keine Gleichung, sondern nur x1, x2 usw. angezeigt statt einer Funktionsgleichung.