[Taylorpolynom Aufgabe] Zeigen Sie: sqrt(x+1) = sqrt(x)

Question

Ziegen Sie:
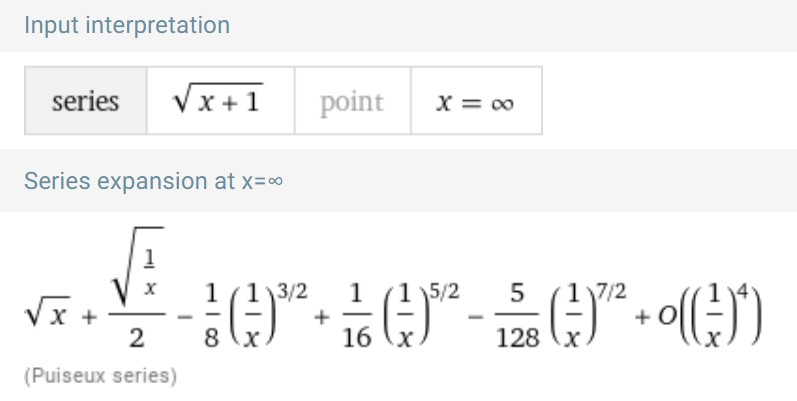
\(\sqrt{x+1} = \sqrt{x} + O(\frac{1}{\sqrt{x}}), \ x \rightarrow ∞ \)

Ich weiß, dass ich das mit einer Taylorreihe lösen soll (wahrscheinlicher erster Ordnung). Nur weiß ich nicht wie ich das mit dem Entwicklungspunkt ∞ machen soll... Kann den ja schlecht einsetzten.

Answer 1

Schreibe \(\sqrt{x+1} = \sqrt x \cdot \sqrt{1+\frac 1{\sqrt x}}\).

Und jetzt entwickle \(\sqrt{1+t}\) um \(t_0=0\) und setze dann \(t=\frac 1{\sqrt x}\) ein.