Zeige, dass die beiden Dreiecke ∆ABC und ∆ADC ähnlich zueinander sind.

Question

Aufgabe:

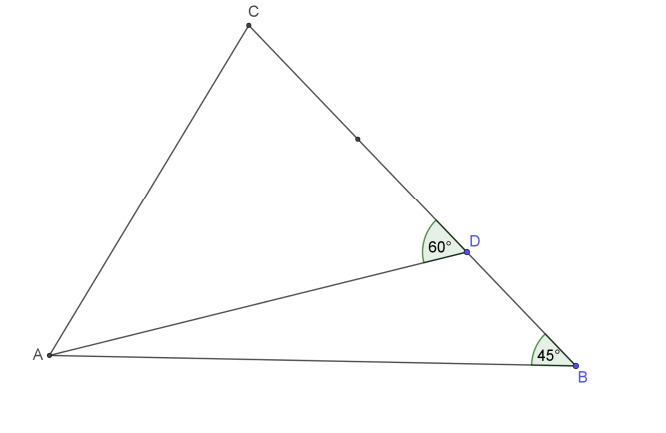
Gegeben sei ein Dreieck ∆ABC und ein Punkt D auf BC, der diese Seite im Verhältnis
|BD|:|DC| = 1: 2 teilt. Weiters kennt man die Winkel ∠CBA = 45° und ∠CDA = 60°. Man
zeige, dass die beiden Dreiecke ∆ABC und ∆ADC ähnlich zueinander sind.

Problem/Ansatz:

Aus der WInkelsumme eines Dreiecks, weiß ich die Winkel des unteren Dreiecks. Da komm ich aber nicht weiter. Außerdem hat mich das Beispiel etwas an den Strahlensatz erinnert. Da habe ich jedoch auch noch keine sinnvolle Anwendung gefunden. Gibt es Ideen?

Comments

Benutze Trigonometrie, um |AC| = √6·|BD| nachzuweisen.

Answer 1

Errichte über den mittleren Drittel DE der Strecke BC ein gleichseitiges Dreieck, dessen dritter Punkt S im Inneren des Dreiecks ABC verläuft. Verbinde S mit B und mit C. Berechne die Innenwinkel der kongruenten Dreiecke BDS und CSE.

Nutze die erhaltenen Werte, um auch die Innenwinkel der beiden übrigen Teildreiecke zu berechnen.

Comments

Ok, so funktioniert das natürlich, danke. Warum ist der Punkt S gleichzeitig der Schwerpunkt des Dreiecks? Hat das mit den Verhältnissen zu tun?

---

Warum ist der Punkt S gleichzeitig der Schwerpunkt des Dreiecks?

der oben eingezeichnete Punkt \(S\) ist nicht der Schwerpunkt. Es ist der Umkreismittelpunkt von \(\triangle ABC\)

---

Ach ja, das war ein Denkfehler. Aber gibt es eine Begründung, warum der konstruierte Punkt gleichzeitig der Umkreismittelpunkt ist?

---

Aber gibt es eine Begründung, warum der konstruierte Punkt gleichzeitig der Umkreismittelpunkt ist?

Wegen der Dreiteilung von \(BC\) und wegen der Symmetrie des gleichseitigen Dreiecks \(\triangle SDE\) muss \(S\) auf der Mittelsenkrechten von \(BC\) liegen (schwarz gestrichelt). Daraus folgt: \(|SB| = |SC|\)

Und wenn Du den Beweis - wie von abakus beschrieben - durchgeführt hast, so hast Du doch auch die Winkel \(\angle BAS\) und \(\angle SBA\) berechnet. Diese sind beide \(=15°\). Daraus folgt, dass das Dreieck \(\triangle ABS\) gleichschenklig ist - bzw. \(|SA|=|SB|\).