Aufgabe:
Text erkannt:
Eine Gartenarchitektin erhält den Auftrag, für einem Spielpark eine neue Rutsche zu entwerfen.
In einer Planungsskizze wählt sie ein Koordinatensystem so, dass der Startpunkt \( \mathbf{A} \) der Rutsche auf der \( y \)-Achse und der Endpunkt E der Rutsche auf der X-Achse liegt.
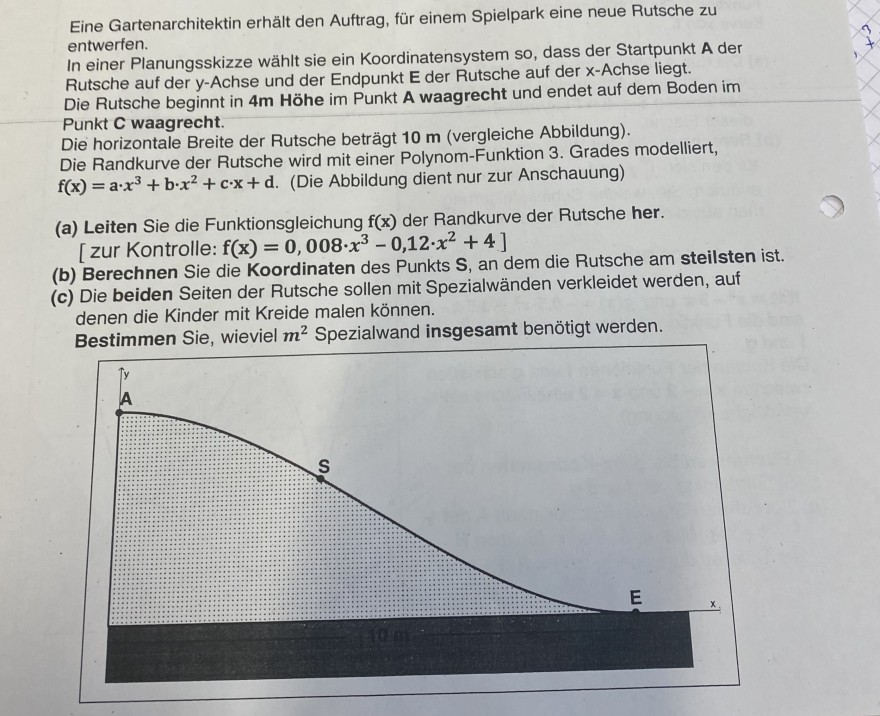
Die Rutsche beginnt in \( 4 \mathrm{~m} \) Höhe im Punkt A waagrecht und endet auf dem Boden im Punkt C waagrecht.
Die horizontale Breite der Rutsche beträgt \( 10 \mathrm{~m} \) (vergleiche Abbildung).
Die Randkurve der Rutsche wird mit einer Polynom-Funktion 3. Grades modelliert, \( f(x)=a \cdot x^{3}+b \cdot x^{2}+c \cdot x+d \). (Die Abbildung dient nur zur Anschauung)
(a) Leiten Sie die Funktionsgleichung \( \mathrm{f}(\mathrm{x}) \) der Randkurve der Rutsche her. [ zur Kontrolle: \( \mathrm{f}(\mathrm{x})=\mathbf{0}, \mathbf{0 0 8} \cdot \boldsymbol{x}^{3}-\mathbf{0 , 1 2} \cdot \boldsymbol{x}^{2}+\mathbf{4} \) ]
(b) Berechnen Sie die Koordinaten des Punkts S, an dem die Rutsche am steilsten ist.
(c) Die beiden Seiten der Rutsche sollen mit Spezialwänden verkleidet werden, auf denen die Kinder mit Kreide malen können.
Bestimmen Sie, wieviel \( m^{2} \) Spezialwand insgesamt benötigt werden.
