Aufgabe:
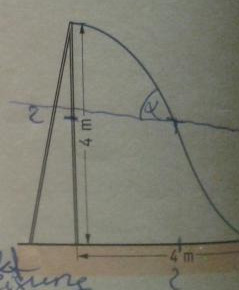
Das Bild zeigt den Entwurf einer Metallrutsche für Spielplätze. Das seittiche Profil der Rutsche soll durch den Graphen
einer ganzrationalen Funktion modelliert werden und durch deren Extrempunkte begrenzt sein.
a) Bestimmen Sie einen geeigneten Funktionsterm.
b) Der TÜV fordert von den Herstellern, dass Spielzeugrutschen an keiner Stelle steiler sein dürfen als 50° gegen die Horizontale. Entspricht die Rutsche dieser Anforderung?
c) Entwerfen Sie eine 4 m hohe Rutsche, deren Steigung an der steilsten Stelle genau 45° beträgt.
Die Funktionsgleichung zu a ist:
f(x) = 1/8x3 - 3/4x2 + 4
Wendepunkt in (2|2)
Ich verstehe Aufgaben b und c nicht.