Wie groß ist die Seitenlänge des Quadrats?

Question

Aufgabe:

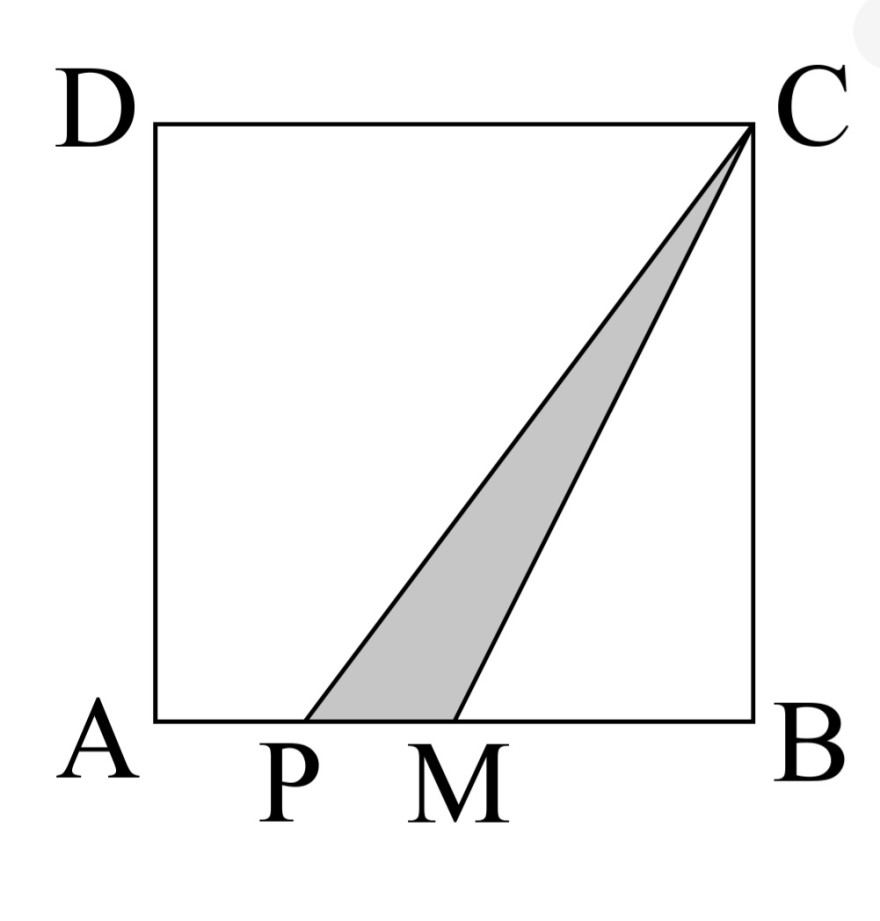
Gegeben ist das Quadrat ABCD mit dem Flächeninhalt von 64 cm². M ist der Mittelpunkt der Strecke AB. P ist der Mittelpunkt der Strecke AM.

a) Wie groß ist die Seitenlänge des Quadrats? b) Welcher Anteil des Quadrates ist grau gefärbt?

Problem/Ansatz:

Also bei a.) 8 cm raus, weil das ja ein Quadrat ist und da müssen die Seiten gleich lang sein. Für M habe ich 4cm, weil das der Mittelpunkt von der Strecke AB ist und für P habe ich 2 cm raus.

Jetzt wollte ich den Trapez (links) und dreieck (rechts) ausrechnen, damit ich dann die beiden Flächeninhalt vom Quadrat abziehen kann, dann habe ich ja das grau markierte. Ich habe aber für den Trapez 64 cm² und für das Dreieck 16cm² aber das geht ja nicht auf. Kann mir hier jemand weiterhelfen?

Answer 1

mach es nicht so kompliziert, vom grauen Dreieck hast du die Grundlinie, also die Strecke PM= 2 cm und die Höhe= 8 cm. Jetzt kann die einfachste Formel für eine Dreiecksfläche angewendet werden.

Comments

Warum ist die Höhe 8 cm?

---

Dreieck und Quadrat haben die gleiche Höhe.

---

Ok. Aber das Dreieck ist ja quasi schief. Wie weiß man, dass die Höhe 8 cm ist?

Answer 2

a^2 = 64

a= 8 = h

AM= 4cm

AP= 2 cm

A(PBC) = 0,5* 6*8 = 24 cm^2

A(MBC) = 0,5*4*8 = 16 cm^2

-> graue Fläche = 8 cm^2

8/64 = 1/8 = 0,125 = 12,5%

Comments

Ich verstehe noch nicht ganz warum die Höhe vom Dreieck 8cm ist

---

AB = BC

Im reckwinklige Dreieck kann die Katheten als Grundlinie und Höhe verwenden.

Für die Fläche gilt: A= (g*h)/2

---

Alle Dreieck haben eine Höhe von 8 cm (und damit übrigens auch den gleichen Flächeninhalt) :

 

Answer 3

Angeregt durch den Kommentar von Gast hj2166  bin ich mal von einem Parallelogramm mit \(a=8, b=8,54 , h=8 \) ausgegangen. Da ergibt sich die gleiche Flächengröße wie beim Quadrat.