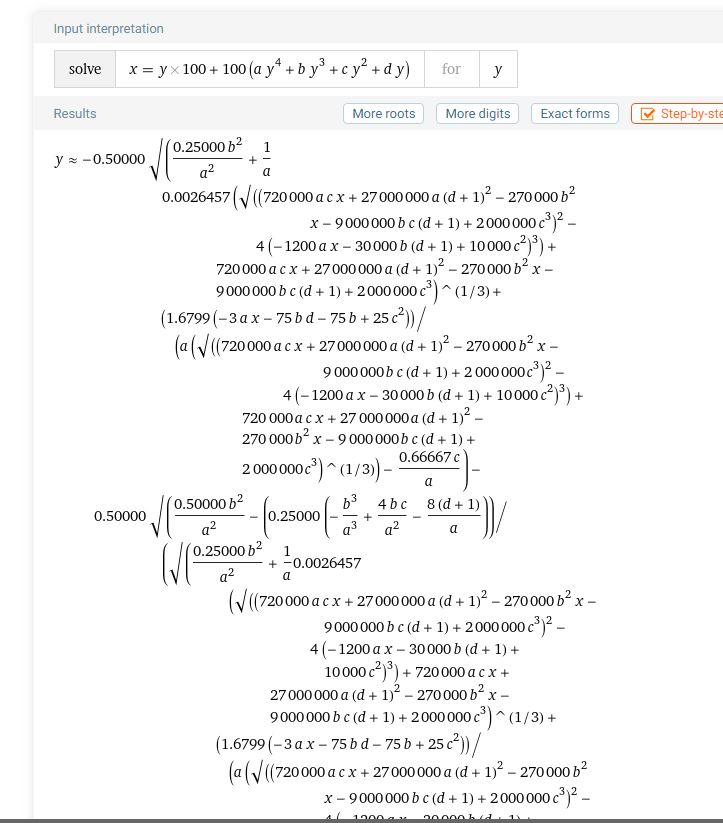
Text erkannt:
Input interpretation
solve \( \quad x=y \times 100+100\left(a y^{4}+b y^{3}+c y^{2}+d y\right) \)
for
\( y \)
Results
More roots
More digits
Exact forms
\( \begin{array}{l} \left(\sqrt{\left(\frac{0.25000 b^{2}}{a^{2}}+\frac{1}{a} 0.0026457\right.}\right. \\ \left(\sqrt { } \left(\left(720000 a c x+27000000 a(d+1)^{2}-270000 b^{2} x-\right.\right.\right. \\ \left.9000000 b c(d+1)+2000000 c^{3}\right)^{2}- \\ 4(-1200 a x-30000 b(d+1)+ \\ \left.\left.10000 c^{2}\right)^{3}\right)+720000 a c x+ \\ 27000000 a(d+1)^{2}-270000 b^{2} x- \\ \left.9000000 b c(d+1)+2000000 c^{3}\right) \wedge(1 / 3)+ \\ \left(1.6799\left(-3 a x-75 b d-75 b+25 c^{2}\right)\right) / \\ \left(a \left(\sqrt { } \left(\left(720000 a c x+27000000 a(d+1)^{2}-270000 b^{2}\right.\right.\right.\right. \\ \left.x-9000000 b c(d+1)+2000000 c^{3}\right)^{2}- \\ \end{array} \)