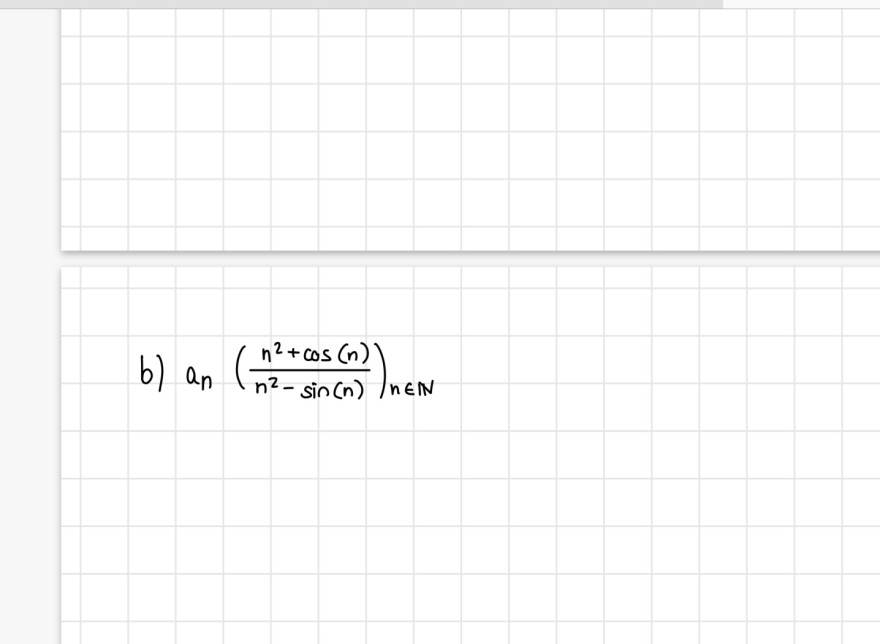
Text erkannt:
b) \( a_{n}\left(\frac{n^{2}+\cos (n)}{n^{2}-\sin (n)}\right)_{n \in \mathbb{N}} \)
Aufgabe:
Hallo, ich möchte bei dieser Folge den Grenzwert mithilfe des Sandwichsatzes bestimmen. Wie kann ich vorgehen, wenn ich trigonometrische Funktionen wie bei diesem Beispiel habe?
LG