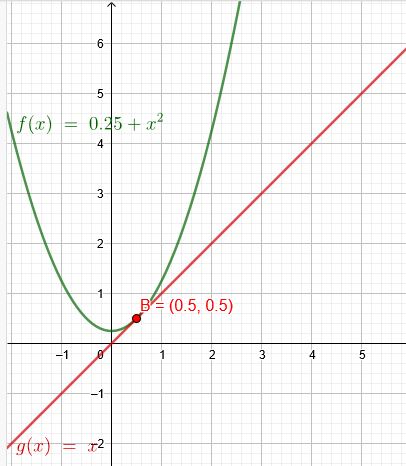
Wie muss a gewählt werden, damit der Graph von \(f(x)=a+x^2\) die Winkelhalbierende \(g(x)=x\) berührt?
\(a+x^2=x\)
\(x^2-1x=-a\)
\(x-0,5)^2=-a+0,5^2=0,25-a\)
\(x-0,5=\sqrt{0,25-a}\)
Berührung liegt dann vor, wenn \(\sqrt{0,25-a}=0\) → \(a=0,25\)
\(f(x)=0,25+x^2\)
Wie lautet die Gleichung der Berührtangente?
\(x-0,5=\sqrt{0,25-0,25}=0\)
\(x=0,5\) \(y=0,5\) Steigung an der Stelle \(x=0,5\) → \(g´(0,5)=1\)
\( \frac{y-0,5}{x-0,5}=1 \)
\( y=x-0,5+0,5=x \)