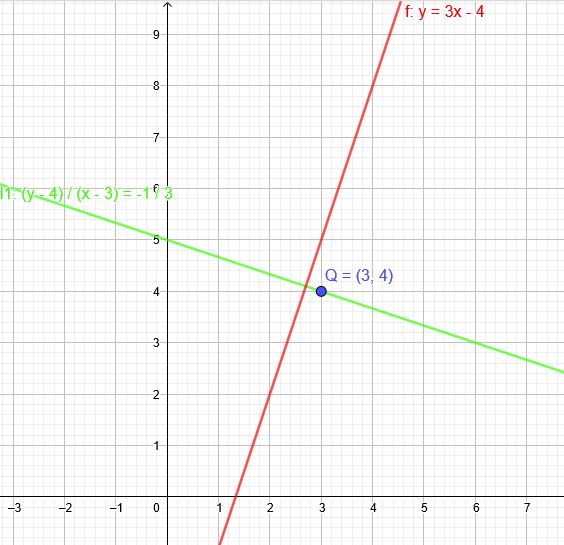
Welche Gleichung hat die Orthogonale g zur Geraden?

Question

Aufgabe:

Welche Gleichung hat die Orthogonale g zur Geraden mit y= 3x-4 durch Q (3/4) ?

Problem/Ansatz:

Wie geht man da vor, soll ich am Besten das Einsetzen benutzen oder nach x auflösen?

Bitte um Euer Rat, liebe Mathelounge :)

Answer 1

g(x) = m*x+b

m= -1/y'(3) = -1/3

Q einsetzen:

-1/3*3 +b = 4

b= 5

g(x) = -1/3*x+5

Comments

vielen Dank für Deine Hilfe :)

Answer 2

die Ursprungsgleichung hat die Steigung 3, damit hat die Ortogonale die Steigung -1/3. Jetzt muss nur noch ein additiver Wert gefunden werden, damit die Gerade durch Q=(3|4) läuft.

Comments

Danke vielmals :)

Answer 3

Welche Gleichung hat die Orthogonale g zur Geraden mit \(y= \red{3}x-4\) durch \(Q (\blue{3}|\green{4})\) ?

Die Gerade hat die Steigung \(m=\red{3}\)

Die Orthogonale zu dieser Geraden hat die Steigung \(m_O=- \frac{1}{\red{3}} \)

\( \frac{y-\green{4}}{x-\blue{3}}=- \frac{1}{\red{3}} \)

Nun nach y auflösen.

Comments

vielen lieben Dank für Deine Hilfe ;)