Konvergenz einer Potenzreihe?

Question

Wir sollen folgende Potenzreihe in Abhängigkeit von x ∈ R und c ∈ R\{0} auf Konvergenz untersuchen.

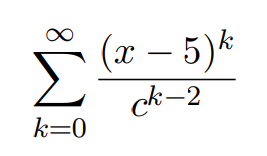
Text erkannt:

\( \sum \limits_{k=0}^{\infty} \frac{(x-5)^{k}}{c^{k-2}} \)

Ich habe folgendes versucht:

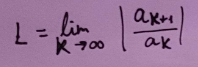
Text erkannt:

\( L=\lim \limits_{k \rightarrow \infty}\left|\frac{a_{k+1}}{a_{k}}\right| \)

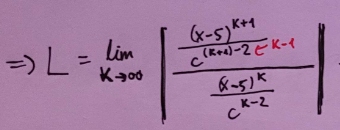
Text erkannt:

\( \Rightarrow L=\lim \limits_{k \rightarrow \infty}\left|\frac{\frac{(x-5)^{k+1}}{c^{(k+1)-2 e^{k-1}}}}{\frac{(x-5)^{k}}{c^{k-2}}}\right| \)

nun müssen wir noch noch |x-5/c| nach < 1, >1 & =1 umstellen?

Answer 1

Hallo

1. c^2 aus der summe Zeihen, dann |(x-5)/ck|<1 für k> ein N0, dannHat man das Verhalten einer geometrischen Reihe d.h natürlich auch lim |(x-5)/ck|<1

Gruß lul