Häufungspunkte bestimmen

Question

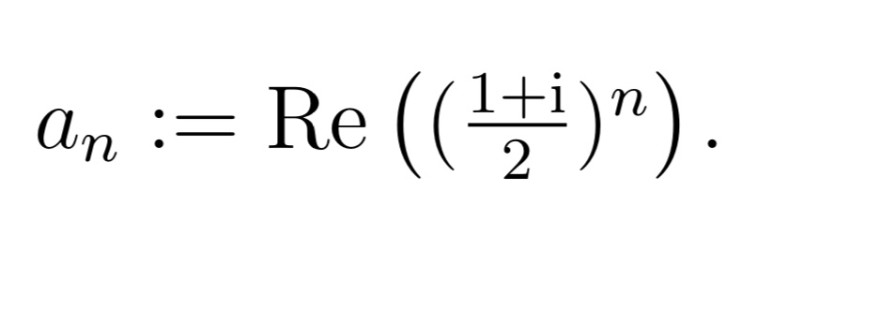
Text erkannt:

\( a_{n}:=\operatorname{Re}\left(\left(\frac{1+\mathrm{i}}{2}\right)^{n}\right) \).

Aufgabe:

kann mir bitte jemand erklären, wie man hier die Häufungspunkte bestimmen kann? Ich bin bis jetzt so vorgegangen, dass ich mir jeweils die Teilfolgen 2k und 2k+1 herausgeschrieben habe aber komme leider nicht auf die Häufungspunkte.

Comments

Ich würde die komplexe Zahl (1+i)/2 in Polarkoordinaten darstellen, daraus die Polarkoordinatendarstellung der Potenzen ableiten und daraus den Realteil. Dann solltest Du sehen, was passiert

---

Das habe ich bereits gemacht und komme auf 1/sqrt(2)*cos(pi/4n). Wenn ich jetzt aber den Verlauf für gerade/ ungerade Zahlen anschaue, komme ich nicht auf das richtige ergebnis

---

Du ahst die Potenz bei 1/sqrt(2) vergessen, vgl. die Tabelle von Roland

Answer 1

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14
an	\( \frac{1}{2} \)	0	-\( \frac{1}{4} \)	-\( \frac{1}{4} \)	-\( \frac{1}{8} \)	0	\( \frac{1}{16} \)	\( \frac{1}{16} \)	\( \frac{1}{32} \)	0	-\( \frac{1}{64} \)	-\( \frac{1}{64} \)	-\( \frac{1}{128} \)	0

Die Minuszeichen über den Brüchen gehören vor die Brüche.