Die Winkelhalbierende teilt die gegenüberliegende Seite im Verhältnis der anliegenden Seiten.
Aus u:(u+3) = b:(b+5) folgt nach wenigen Umformungen u:b=3:5.
Wir nehmen uns eine beliebige Streckenlänge x und konstruieren ein Dreieck A'D'C' mit
A'D'=3x, A'C'=5x und Winkel A'C'D'=35° (zwei Lösungen, weil der Winkel der kleineren Seite gegenüberliegt. An A'C' wird erneut ein 35°-Winkel angetragen, dessen freier Schenkel die gerade A'D' im B' schneidet.
Auf der Strecke D'B' wird der Punkt S festgelegt mit A'D' = D'S.
Auf dem Strahl SB' wird der Punkt B mit SB=3 festgelegt.
Eine zentrische Streckung des Dreiecks A'B'C' mit Zentrum S, die B' in B überführt, erzeugt das gewünschte Dreieck ABC.
PS: Es geht ja noch VIEL einfacher:
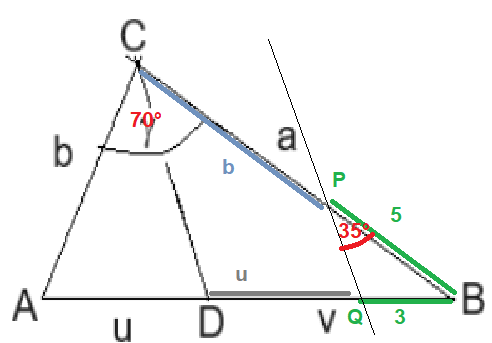
Nicht nur u und b verhalten sich wie 3:5, sondern auch v und a.
Wenn man auf BC die Länge b und auf DB die Länge v abträgt, erhält man die eingezeichneten Punkte P und Q, und die Restlängen QB und PB verhalten sich ebenfalls wie 3:5, denn sie sind 3 und 5.
Damit ist PQ parallel zu CD, und wir bekommen den rot eingezeichneten 35°-Stufenwinkel. Das Dreieck QBP ist damit (in zwei nicht kongruenten Varianten) konstruierbar.
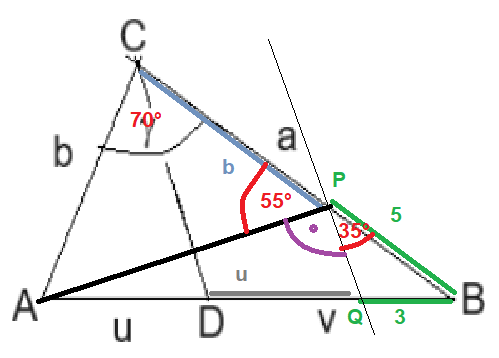
Im gleichschenkligen Dreieck APC ergibt sich der rot eingezeichnete 55°-Winkel, und der violett eingezeichnete Winkel hat die Größe von 180°-55°-35°=90°.Die Senkrechte zu PQ durch P schneidet die Gerade BQ in A
Die Gerade PB schneidet die Mittelsenkrechte von AP in C.
Geile Aufgabe!