Reihen, Binomialkoeffizienten, bin.-Lehrsatz

Question

Text erkannt:

$a_{n}=\left(1+\frac{1}{n}\right)^{n}, \quad b_{n}=\sum \limits_{k=0}^{n} \frac{1}{k !}, \quad n \in \mathbb{N} .$

Setzen wir e $:=\exp (1)$, so wissen wir aus der Vorlesung, dass $\lim \limits_{n \rightarrow \infty} b_{n}=$ e. Zeigen Sie nun
(a) $2 \leq b_{n}<3, n \in \mathbb{N}$,
(b) $a_{n} \leq b_{n}, n \in \mathbb{N}$,
(c) $\lim \limits_{n \rightarrow \infty} a_{n}=\lim \limits_{n \rightarrow \infty} b_{n}=\mathrm{e}$.

Hinweis zu (b) und (c): Zeigen Sie mithilfe des binomischen Lehrsatzes
$a_{n}=\sum \limits_{k=0}^{n}\left(\frac{1}{k !} \prod \limits_{j=0}^{k-1}\left(1-\frac{j}{n}\right)\right) .$

Seien Sie unbesorgt: das Produkt lässt sich leicht abschätzen. Vergleichen Sie die Summanden mit den Summanden von $b_{n}$. Grenzwerte von Folgen sind gleich, wenn die Differenz der Folgen eine Nullfolge ist.

Aufgabe: es geht um die Aufgabe b

Problem/Ansatz: ich verstehe das grundlegende Vorgehen mit dem bin-Lehrsatz, aber beim auseinanderziehen des binomialkoeffizienten komme ich nicht weiter. Wie muss ich da weiter vorgehen?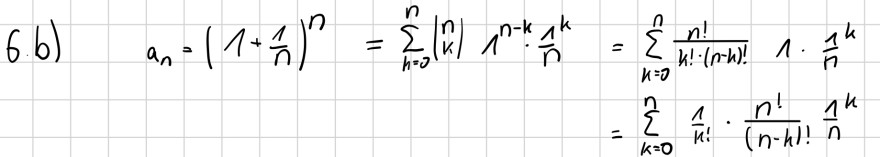

Text erkannt:

6.b) $\quad \begin{aligned} a_{n}=\left(1+\frac{1}{n}\right)^{n}=\sum \limits_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array} \mid 1^{n-k} \cdot 1^{k}\right. & =\sum \limits_{k=0}^{n} \frac{n !}{k ! \cdot(n-k) !} 1 \cdot \frac{1}{n}^{k} \\ & =\sum \limits_{k=0}^{n} \frac{1}{k !} \cdot \frac{n !}{(n-k) !} \frac{1}{n}^{k}\end{aligned}$

Answer 1

$\frac{n!}{(n-k)!}= \frac{\prod\limits_{i=1}^n i}{\prod\limits_{i=1}^{n-k}i}=\prod\limits_{i=0}^{k-1} (n-i)$

In der Summe haben wir noch $n^k$ im Nenner, ziehe das ins Produkt.

Bei Deinem $(\frac1n)^k$ fehlen Klammern, solche Nachlässigkeiten machen solche Aufgaben schwierig.

Comments

OK den ersten Schritt mit den Produkten verstehe ich. Aber wie kommt man von da zu dem einheitlichen Produkt?

Ansonsten danke schon mal:)

---

Regel, die bei Summen/Produkten oft hilft:
Schreibe die beiden Produkte aus (es ist ja nicht magisches, nur ein Abkürzungszeichen).