Aufgabe:
Die ersten drei Ableitungen der Aufgabe c)
Problem/Ansatz:
Verstehe diese Aufgabe nicht habe irgendwo einen Denkfehler.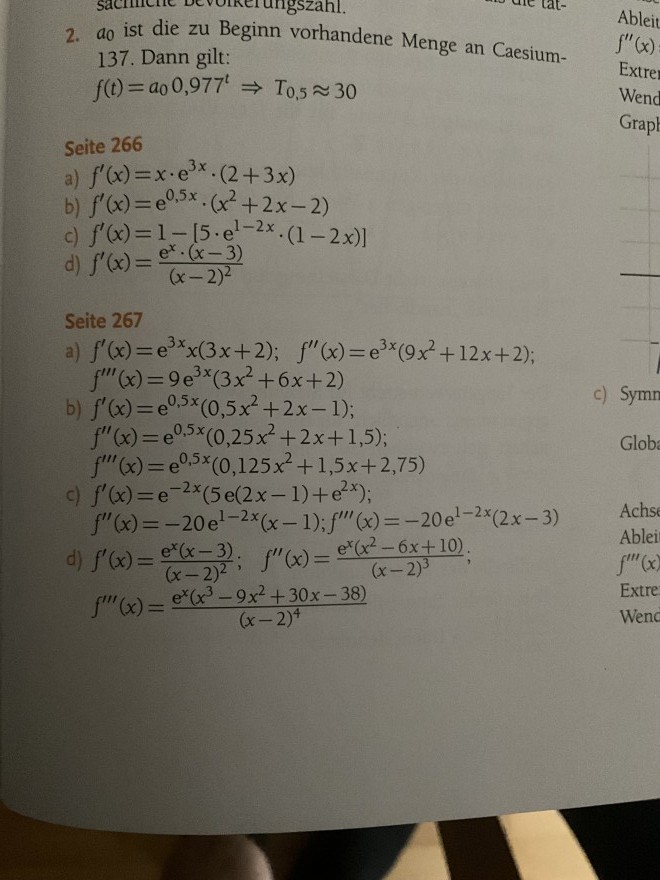
Text erkannt:
2. \( a_{0} \) ist die zu Beginn vorhandene Menge an Caesium137. Dann gilt:
\( f(t)=a_{0} 0,977^{t} \Rightarrow T_{0,5} \approx 30 \)
Seite 266
a) \( f^{\prime}(x)=x \cdot e^{3 x} \cdot(2+3 x) \)
b) \( f^{\prime}(x)=e^{0,5 x} \cdot\left(x^{2}+2 x-2\right) \)
c) \( f^{\prime}(x)=1-\left[5 \cdot e^{1-2 x} \cdot(1-2 x)\right] \)
d) \( f^{\prime}(x)=\frac{e^{x} \cdot(x-3)}{(x-2)^{2}} \)
Seite 267
a)
\( \begin{array}{l} f^{\prime}(x)=e^{3 x} x(3 x+2) ; \quad f^{\prime \prime}(x)=e^{3 x}\left(9 x^{2}+12 x+2\right) \\ f^{\prime \prime \prime}(x)=9 e^{3 x}\left(3 x^{2}+6 x+2\right) \end{array} \)
b)
\( \begin{array}{l} f^{\prime}(x)=e^{0,5 x}\left(0,5 x^{2}+2 x-1\right) \\ f^{\prime \prime}(x)=e^{0,5 x}\left(0,25 x^{2}+2 x+1,5\right) \\ f^{\prime \prime \prime}(x)=e^{0,5 x}\left(0,125 x^{2}+1,5 x+2,75\right) \end{array} \)
c)
\( \begin{array}{l} f^{\prime}(x)=\mathrm{e}^{-2 x}\left(5 \mathrm{e}(2 x-1)+\mathrm{e}^{2 x}\right) \\ f^{\prime \prime}(x)=-20 \mathrm{e}^{1-2 x}(x-1) ; f^{\prime \prime \prime}(x)=-20 \mathrm{e}^{1-2 x}(2 x-3) \end{array} \)
d)
\( \begin{array}{l} f^{\prime}(x)=\frac{e^{x}(x-3)}{(x-2)^{2}} ; \quad f^{\prime \prime}(x)=\frac{e^{x}\left(x^{2}-6 x+10\right)}{(x-2)^{3}} \\ f^{\prime \prime \prime}(x)=\frac{e^{x}\left(x^{3}-9 x^{2}+30 x-38\right)}{(x-2)^{4}} \end{array} \)

Text erkannt:
\( f(x)=\frac{x+1}{e^{x}}=(x+1) \cdot e^{-x} \) kann auch mit der Produkt-und Kettenregel abgeleltet werden.
n Funktionen ir verwenden leitungsfunk-
en mit den geeigneten Ableitungsregeln.
2) \( \cdot e^{0,5 x} \)
c) \( f(x)=x-5 x \cdot \mathrm{e}^{1-2 x} \)
c) \( f(x)=x-5 x \cdot e^{1-2 x} \)
d) \( f(x)=\frac{e^{x}}{x-2} \)
en Exponentialfunktion
in Bezug auf Symmetrie und Globalverlauf, auf Achsenschnittpun eichnen Sie den Graphen.
etrisch zur \( y \) ordinatenur-
kleiner WerUnendlichen:
\( \begin{array}{l} f(x)=\frac{x+1}{\mathrm{e}^{x}} \Rightarrow f(x)=\frac{u(x)}{v(x)} \\ u(x)=x+1 \Rightarrow u^{\prime}(x)=1 \\ v(x)=\mathrm{e}^{x} \quad \Rightarrow v^{\prime}(x)=\mathrm{e}^{x} \\ \text { - } f^{\prime}(x)=\frac{u^{\prime}(x) \cdot v(x)-u(x) \cdot v^{\prime}(x)}{[v(x)]^{2}} \\ f^{\prime}(x)=\frac{1 \cdot e^{x}-(x+1) \cdot e^{x}}{\left[e^{x}\right]^{2}}=\frac{e^{x} \cdot(1-(x+1))}{\left[e^{x}\right]^{2}}=\frac{-x}{e^{x}} \\ \end{array} \)
Ausklammern und Kürzen