Riemannsche Zwischensumme einzeichnen (Ober- und Untersumme)

Question

Sei f(x) = -x² + 2x + 3 (s. Skizze).

Berechnen Sie (mit einem Taschenrechner) Näherungen zu $$ \int \limits_{0}^{3} f(x) dx $$ durch eine Riemannsche Zwischensumme zu den folgenden Zerlegungen

a) x0 = 0, x1 = 1, x2 = 2, x3 = 3,

b) x0 = 0, x1 = 0.5, x2 = 1, x3 = 1.5, x4 = 2, x5 = 2.5, x6 = 3,

c) x0 = 0, x1 = 1, x2 = 2.5, x3 = 3

und Zwischenstellen xk am linken Intervallrand.

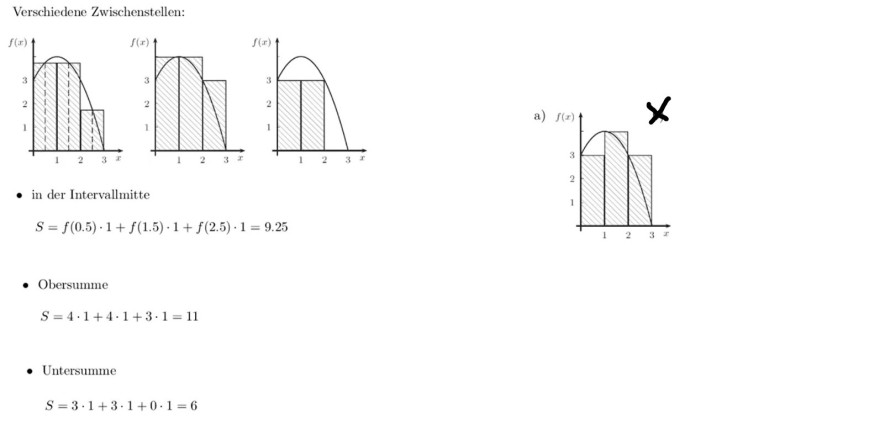
Was ergibt sich bei der Zerlegung a) bei Zwischenstellen xk in der Intervallmitte bzw. als Ober- und Untersumme?

Skizzieren SIe die Situationen.

Den ersten Teil der Aufgabe habe ich bereits verstanden und gelöst.

Den zweiten Teil der Aufgabe (Was ergibt sich bei der Zerlegung...)

Ich weiß nicht, wie ich die Intervallmitte, Ober- und Untersumme bestimmen soll. Zeichnung weiß ich auch überhaupt nicht von den 3 gesuchten Sachen. a) an sich konnte ich richtig einzeichnen (a) ist auf der rechten Seite der Lösung dargestellt)

Dann weiß ich auch nicht, wie ich die jeweiligen Werte in die Formel einsetzen soll. Konkret sieht die Lösung so aus:

Answer 1

Die Intervallmitte ist halt der Wert in der Mitte des Intervalls... Ich weiß ehrlich gesagt nicht, was das genaue Problem ist. Spätestens mit der vorhandenen Lösung sollte das doch klar sein. Und a) klappt, aber der Rest nicht? Und was ist an der Zeichnung unklar? Zeichne die Parabel und zeichne die Stellen ein und bilde dann die Rechtecke. Du hast da in der Lösung doch ein Beispiel. Warum orientierst du dich nicht daran?