Text erkannt:
\( a-0,4 k a=0 \quad 1+0,4 k \)
1.4
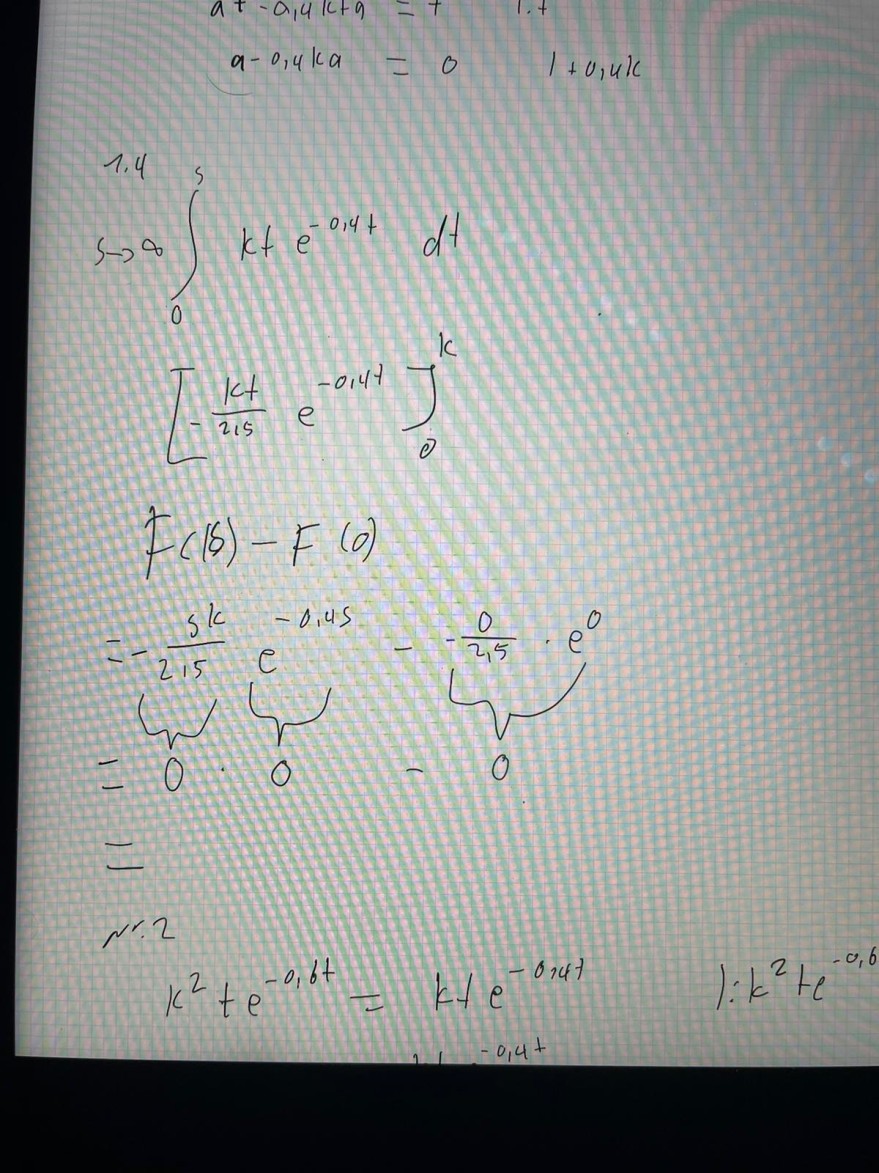
\( \begin{array}{l} \operatorname{si\infty }_{s \rightarrow \infty}^{1,4} k t e^{-0,4 t} d t \\ {\left[-\frac{k t}{215} e^{-0,4 t}\right]_{0}^{k}} \\ F(\beta)-F(0) \\ =-\frac{5 k}{2,15} e^{-0,45}-\underbrace{-\frac{0}{2,5}}_{0} \cdot e^{0} \\ \text { - } \\ \text { Nr. } 2 \\ \end{array} \)
\( k^{2} t e^{-0,6 t}=k t e^{-0,4 t} \quad l: k^{2} t e^{-0,6} \)

Text erkannt:
\( \begin{array}{l} f^{\prime \prime}(2,5)=0,4 k e^{-1}-2 k e^{-1} \\ k>0 \\ f^{\prime \prime}(2,5)<0 \end{array} \)
1. 3
\(
\begin{array}{l}
1.3 \\
F_{k}(t)=k \cdot(a \cdot t+b) \cdot e^{-0,4 t} \\
F_{k}^{\prime}(t)=(a t+b) \cdot e^{-0,4 t}+k \cdot a \cdot e^{-0,4 t}+k \cdot(a t+b)-0,4 e^{-0,4 t} \\
F_{k}^{\prime}(t)=a t e^{-0,4 t}+b e^{-0,4 t}+k a e^{-0,4 t}+k a t+k t \cdot-0,4 e^{-0,4 t} \\
\left.F_{k}^{\prime}(t)=e^{-0,4 t}(a t+b+k a t-0,4) k(a t+b)\right) \\
\quad-0,4 k t a-0,4 k b \\
a t-0,4 k t a=t \quad 1: t \\ a-0,4 k a=0 \quad 1+0,4 k \end{array}
\)
\( \begin{array}{c} \sin _{0 \rightarrow \infty}^{1.4} k t e^{-0,4 t} d t \\ {\left[-\frac{k t}{2.5} e^{-0,4 t}\right]_{0}^{k}} \end{array} \)