Rang und Matrizen-lineare Gleichungssysteme

Question

Hallo ich komme mit dieser Aufgabe nicht zurecht:

Seien A∈K^l,m, B∈K^m,n. Zeigen Sie, dass dann RangA+RangB≤m+Rang(AB) gilt.

Was muss ich denn hier machen, was bedeutet m? Kann ich das m auch irgedwie auf die andere Seite der Ungleichung bringen?

Wär nett wenn mir jemand helfen könnte bei der Lösung!

Vielen Dank schon mal!

Comments

Wenn man zwei Matrizen miteinander multiplizieren will, müssen die Zeilen der ersten gleich lang sein wie die Spalten der zweiten. m steht für die Zeilenlänge der ersten und die Spaltenlänge der zweiten Matrix. m ist also eine natürliche Zahl. Du könntest sie mittels Subtraktion auf die andere Seite bringen.
Ich hoffe jetzt mal, dass dir das irgendwie hilft.

Answer 1

Seien A∈Kl,m, B∈Km,n. Zeigen Sie, dass dann RangA+RangB≤m+Rang(AB) gilt.

RangA+RangB≤m+Rang(AB)

RangA ≤ min (l,m)

RangB ≤ min (m,n)

RangAB ≤ min (l,n)

Fall l <m <n

RangA+RangB ≤ l + m

m+Rang(AB) ≤ m + l

Fall n<m<l

RangA+RangB ≤ m + n

m+Rang(AB) ≤ m + n

Ich komme zwar bei beiden Seiten auf die gleiche obere Schranke. Damit ist die Ungleichung noch nicht gezeigt.

 

Vor allem, wenn man noch bedenkt, dass der kleinere von beiden Rängen immer auf der rechten seite der zweiten Gleichung erscheinen muss, denn:

Rang ( AB) ≤ min {RangA, RangB}

 

 

Gemäss Wikipedia https://de.wikipedia.org/wiki/Rang_(Mathematik) 

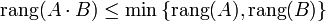
Dafür steht dort wenigstens, dass die Behauptung in dieser Aufgabe immer stimmt.