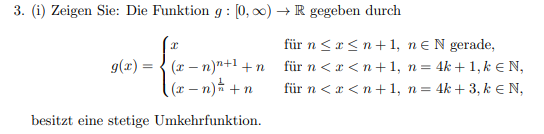
Text erkannt:
3. (i) Zeigen Sie: Die Funktion \( g:[0, \infty) \rightarrow \mathbb{R} \) gegeben durch
\( g(x)=\left\{\begin{array}{ll} x & \text { für } n \leq x \leq n+1, n \in \mathbb{N} \text { gerade, } \\ (x-n)^{n+1}+n & \text { für } n<x<n+1, n=4 k+1, k \in \mathbb{N}, \\ (x-n)^{\frac{1}{n}}+n & \text { für } n<x<n+1, n=4 k+3, k \in \mathbb{N}, \end{array}\right. \)
besitzt eine stetige Umkehrfunktion.
Hi, kann mir jemand helfen zu verstehen wie g(x) definiert ist, ich verstehe das nicht ganz mit den n´s und k´s. Sind das verschiedene Funktionen und man wählt dann einmal generell ein k und ein gerades n? oder wie ist das