Umstellen von Exponenten und Wurzeln

Question

Aufgabe:

Aufgabe 1.

Aufgabe 2.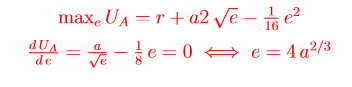

Text erkannt:

$\begin{array}{c}\max _{e} U_{A}=r+a 2 \sqrt{e}-\frac{1}{16} e^{2} \\ \frac{d U_{A}}{d e}=\frac{a}{\sqrt{e}}-\frac{1}{8} e=0 \Longleftrightarrow e=4 a^{2 / 3}\end{array}$

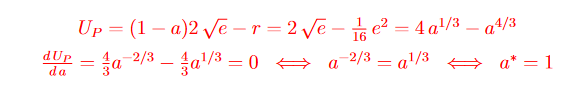
Text erkannt:

$\begin{array}{c}U_{P}=(1-a) 2 \sqrt{e}-r=2 \sqrt{e}-\frac{1}{16} e^{2}=4 a^{1 / 3}-a^{4 / 3} \\ \frac{d U_{P}}{d a}=\frac{4}{3} a^{-2 / 3}-\frac{4}{3} a^{1 / 3}=0 \Longleftrightarrow a^{-2 / 3}=a^{1 / 3} \Longleftrightarrow a^{*}=1\end{array}$

Problem/Ansatz:

Hallo zusammen,

Ich bräuchte eure Hilfe wie man bei der ersten Aufgabe auf das Ergebniss kommt. Bis jetzt habe ich die Ableitung hinbekommen, verstehe jedoch nicht wie man nach der Variable e umstellen soll.

Bei der zweiten Aufgabe wird indiesem Fall e durch 4*a²/3 ersetzt. Leider verstehe ich auch hierbei beim ersten den Rechenvorgang nicht, nachdem man e ersetzt hat. Die Ableitung ist mir aber verständlich.

Bei a*=1, wäre mein Rechenvorgang die beiden Exponenten mit +2/3 zu addieren. Wäre dies möglich?

Answer 1

$\begin{aligned} \frac{a}{\sqrt{e}}-\frac{1}{8}e & =0 & & |+\frac{1}{8}e\\ \frac{a}{\sqrt{e}} & =\frac{1}{8}e & & \text{Def. Potenz mit rationalem Exponent}\\ \frac{a}{e^{\frac{1}{2}}} & =\frac{1}{8}e & & |\cdot e^{\frac{1}{2}}\\ a & =\frac{1}{8}e\cdot e^{\frac{1}{2}} & & \text{Potenzgesetz}\\ a & =\frac{1}{8}e^{1+\frac{1}{2}} & & \text{Bruchrechnung}\\ a & =\frac{1}{8}e^{\frac{3}{2}} & & |\cdot8\\ 8a & =e^{\frac{3}{2}} & & |\square^{\frac{2}{3}}\\ \left(8a\right)^{\frac{2}{3}} & =\left(e^{\frac{3}{2}}\right)^{\frac{2}{3}} & & \text{Potenzgesetz}\\ 8^{\frac{2}{3}}a^{\frac{2}{3}} & =e^{\frac{3}{2}\cdot\frac{2}{3}} & & \text{Bruchrechnung}\\ 8^{\frac{2}{3}}a^{\frac{2}{3}} & =e & & \text{Def. Potenz mit rationalem Exponent}\\ \left(\sqrt[3]{8}\right)^{2}a^{\frac{2}{3}} & =e & & \text{Def. Wurzel}\\ 2^{2}a^{\frac{2}{3}} & =e & & \text{Def Potenz mit natürlichem Exponent}\\ 4a^{\frac{2}{3}} & =e \end{aligned}$

Comments

Könntest du mir noch erklären wie man auf die:

Text erkannt:

$2 \sqrt{e}-\frac{1}{16} e^{2}=4 a^{1 / 3}-a^{4 / 3}$

Wenn man einsetzt?

Text erkannt:

$e=4 a^{2 / 3}$

Text erkannt:

$e=4 a^{2 / 3}$

Answer 2

Bei a*=1, wäre mein Rechenvorgang die beiden Exponenten mit +2/3 zu addieren. Wäre dies möglich?

Entspricht der Multiplikation mit $a^{\frac{2}{3}}$. Das geht nur für $a>0$.

Bei der Ableitung multipliziere mit $\sqrt{e}$.

Den Rest deiner Frage versteht man nicht. Aufgabe 1 fehlt anscheinend.

Comments

Hallo, tut mir leid wegen dem MIssverständniss

Bei Aufgabe 1 wollte ich nur wissen, wie man nach e umstellt.

Text erkannt:

$e=4 a^{2 / 3}$

Text erkannt:

$e=4 a^{2 / 3}$

Was fehlt dir denn genau bei Aufgabe 1?

Text erkannt:

$e=4 a^{2 / 3}$

Bei Aufgabe 2 wird e durch das Ergebniss in Aufgabe 1 ersetzt, also 4*a²/3, und würde ich gerne wissen, wie man auf diese 4*a¹/3 - a⁴/3 kommt.

Text erkannt:

$2 \sqrt{e}-\frac{1}{16} e^{2}=4 a^{1 / 3}-a^{4 / 3}$

Answer 3

HN bilden: 8√e und Zähler Null setzen:

8a- e*√e =0

e^(3/2) = 8a = 2³*a

e = (2^3a)^(2/3) = 2²* a^(2/3) = 4*a^(2/3)