Mein gesunder Menschenverstand setzt manchmal aus in Mathematik , brauche dann Erklärungen ;)
Offensichtlich hattest du ja eine Lösung, die du nur nicht verstanden hast. Aber auch dem Ersteller dieser Lösung fehlte wohl der gesunde Menschenverstand ;)
Das Problem ist manchmal auch, dass den Schülern gesagt wird, bei mehrstufigen Zufallsexperimenten sollte man an Baumdiagramme und Pfadregeln denken.
Das dieses den Schüler verleitet dann evtl. einen Baum zu malen und die Wahrscheinlichkeit damit zu berechnen ist naheliegend. Sollte man auch bei solch kleinen Bäumen mit 2 Stufen noch hinbekommen. Wie gesagt ist es trügerisch wenn man evtl. 5 oder gar 100 Stufen hat.
Hier noch mal ein Baum für genau dein Problem:
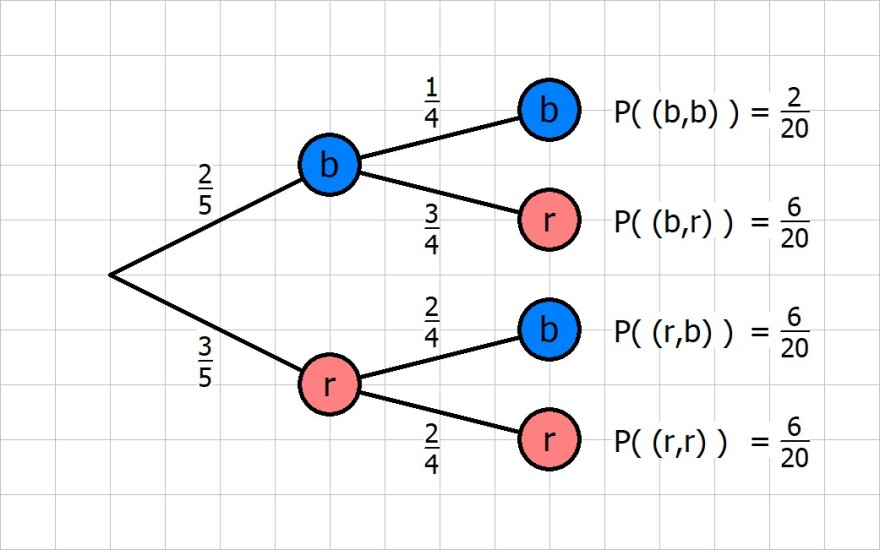
Damit berechnet sich die Wahrscheinlichkeit das die gezogene Kugel blau ist jetzt mit
P(bb, rb) = 2/5 * 1/4 + 3/5 * 2/4 = 2/20 + 6/20 = 8/20 = 2/5
Also natürlich kommt man hier auch rein durch einen Baum auf das korrekte Ergebnis.