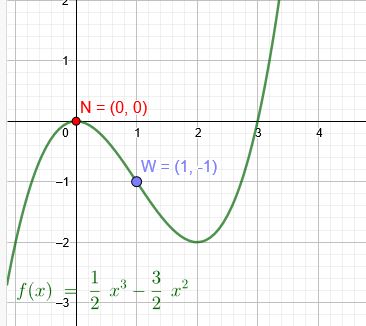
Bestimmen Sie die Funktionsgleichung einer kubischen Funktion y = f(x), die in (0,0) ein lokales Maximum und in (1, …

Question

Aufgabe:

Bestimmen Sie die Funktionsgleichung einer kubischen Funktion y = f(x), die in (0,0) ein lokales Maximum und in (1, −1) einen Wendepunkt hat. Fertigen Sie anschließend eine Skizze der kubischen Funktion f(x) an. Es geht darum die Koeffizienten a, b, c und d herauszufinden, wobei a ≠ 0 ist.

Problem/Ansatz:

f(x) = ax^3+bx^3+cx+d

f'(x) = 3ax^2+2bx+c

f''(x) = 6ax+2b

f(0) = 0

f''(1) = 0

Ich verstehe leider nicht wie ich jetzt die Funktionen voneinander subtrahieren kann und wo genau ich die Wendepunlkte einsetze.

Answer 1

Bestimmen Sie die Funktionsgleichung einer kubischen Funktion \(y = f(x)\), die in \(N(0|0)\) ein lokales Maximum und in \(W(1|−1)\) einen Wendepunkt hat. Fertigen Sie anschließend eine Skizze der kubischen Funktion f(x) an. Es geht darum die Koeffizienten a, b, c und d herauszufinden, wobei a ≠ 0 ist.

Weg über die Nullstellenform der kubischen Parabel:

\(f(x)=a(x-N_1)(x-N_2)(x-N_3)\)

\(N(0|0)\)  lokales Maximum → Somit ist hier eine doppelte Nullstelle:

\(f(x)=ax^2(x-N_3)\)

\(W(1|−1)\)  Wendepunkt  → Der Graph einer kubischen Funktion ist punktsymmetrisch. Somit liegt in \(E(2|-2 )\) das lokale Minimum:

\(f(1)=a(1-N_3)=-1\)  → \(a=\frac{1}{N_3-1}\) 

\(f(x)=\frac{1}{N_3-1}x^2(x-N_3)\)

\(f(2)=\frac{4}{N_3-1}\cdot(2-N_3)=-2\) →  \(\frac{4}{N_3-1}\cdot(N_3-2)=2\)  →  \(N_3=3\)       \(a=\frac{1}{2}\)

\(f(x)=\frac{1}{2}x^2(x-3)\) →   \(f(x)=\frac{1}{2}[x^3-3x^2)]\)  →  \(f(x)=\frac{1}{2}x^3-\frac{3}{2}x^2\)

\(a=\frac{1}{2}\)      \(b=\frac{3}{2}\)    \(c=0\)    \(d=0\)

Answer 2

Es gilt noch \( f'(0)=0 \) und \( f(1)=-1 \). Subtrahiert wird hier gar nichts. Setze die Werte in die entsprechenden Funktionen ein und du erhältst 4 Gleichungen. Löse das LGS. Zum Beispiel mit Gauß.

Comments

Genau das war ja meine Frage; welche Werte setze ich jetzt in welche Funktion um die entsprechenden Koeffizienten ausrechnen zu können?

---

Steht doch da: \( f(0)=0 \) heißt, du setzt 0 in f ein und rauskommen soll 0.

---

aber so komme ich doch nicht auf die Koeffizienten von a b c und d?? ich dachte eigentlich dass ich die Gleichungen voneinander abziehen muss um die jeweiligen Koeffizienten bestimmen zu können

---

Du hast 4 Bedingungen. Das gibt dir 4 Gleichungen. Stelle diese doch erstmal auf. Erst dann schaut man weiter.

---

f(0) = 0*0^3+b*0^2+c*0+d=0
f(1) = 0*1^3+b*1^2+c*1+d=0
f'(0) = 3*0*0^2+2*b*0+c=0
f'' (1) = 6*0*1+2*b=0

0*0+b*0^2+c*0+d=0

d = 0 / b+c+d = 0

-------

3*0*0^2+2b*0+c = 0

c= 0

-----

6*1*1+2b = 0

2b = 0

sinnvoll?

---

Wo ist a? a ist nicht 0. Von der Idee aber gut.

Answer 3

Benutze https://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm zur Hilfe und Selbstkontrolle

Eigenschaften

f(0) = 0
f'(0) = 0
f(1) = -1
f''(1) = 0

Gleichungssystem

d = 0
c = 0
a + b + c + d = -1
6a + 2b = 0

Errechnete Funktion

f(x) = 0,5·x^3 - 1,5·x^2

Skizze

~plot~ 0.5x^3-1.5x^2 ~plot~

Comments

Kannst du bitte nochmal kurz erläutern, wie du auf die Funktion kommst?

---

Entwickel zuerst das LGS. Prüfe mit dem LGS was ich notiert habe.

Löse dann das LGS. Prüfe mit der Lösung die notiert habe.

Solltest du noch Probleme haben sage ganz genau wo deine Probleme im Verständnis liegen.