Aufgabe:
Hey, von mir werden mehrere Fragen kommen, da ich bei diesem Kurztest echt durchstarten muss.
Ich danke euch für die Hilfe!
Gegeben ist die Funktion f in zwei Veränderlichen mit
Die Aufgabe lautet: f(x,y)= (x^2+4x+4)/(y+1)
a) Geben Sie den Definitionsbereich von f an.
Df={(x,y)∈R2|y≠...}
b) Bestimmen Sie eine Funktionsgleichung der Höhenlinie z=1/2.
Problem/Ansatz:
Ich möchte sichergehen, dass diese Aufgabe von mir richtig beantwortet wurde.

Text erkannt:
Gegeben ist die Funktion \( f \) in zwei Veränderlichen mit
\( f(x, y)=\frac{x^{2}+4 \cdot x+4}{y+1} . \)
a) Geben Sie den Definitionsbereich von \( f \) an.
\( \mathbb{D}_{f}=\left\{(x, y) \in \mathbb{R}^{2} \mid y \neq-1\right. \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( -1 \)
b) Bestimmen Sie eine Funktionsgleichung der Höhenlinie \( z=\frac{1}{2} \).
Höhenlinie: \( y(x)=-\mathrm{x}^{\wedge} 2-4^{*} \mathrm{x}-5 \quad \) mit \( \mathbb{D}_{y}=\mathbb{R} \backslash\{-1 \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( -x^{2}-4 \cdot x-5 \)
In Ihrer Antwort wurden die folgenden Variablen gefunden: \( [x] \)
Ihre letzte Antwort wurde folgendermaßen interpretiert:
\( -1 \)
Text erkannt:
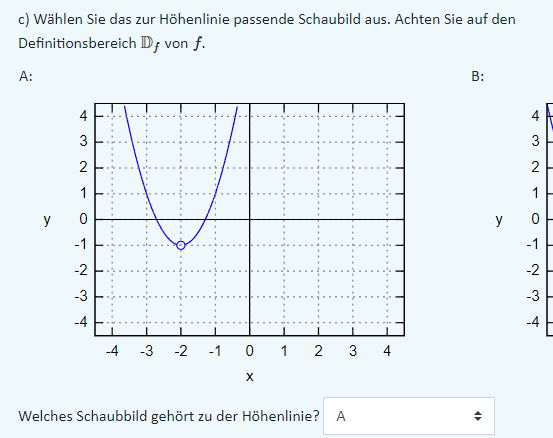
c) Wählen Sie das zur Höhenlinie passende Schaubild aus. Achten Sie auf den Definitionsbereich \( \mathbb{D}_{f} \) von \( f \).
A:
B:
Welches Schaubbild gehört zu der Höhenlinie?
A