Bestimmen einer Funktionsgleichung der Höhenlinie z=\frac{1}{2} .

Question

Hallöchen wiedermal da,

Kann mir wer meine Lösung ansehen und mir sagne ob es richtig ist möglichweiser mir dann eine Lösung geben?

Gegeben ist die Funktion $f$ in zwei Veränderlichen mit
$f(x, y)=\frac{x^{2}+2 \cdot x+1}{y-1} .$
a) Geben Sie den Definitionsbereich von $f$ an.
$\mathbb{D}_{f}=\left\{(x, y) \in \mathbb{R}^{2} \mid y \neq\square\right.$}
b) Bestimmen Sie eine Funktionsgleichung der Höhenlinie $z=\frac{1}{2}$.

Höhenlinie: $y(x)=\square$ mit $\mathbb{D}_{y}=\mathbb{R} \backslash\{ \square$

c) Wählen Sie das zur Höhenlinie passende Schaubild aus. Achten Sie auf den Definitionsbereich $\mathrm{D}_{f}$ von $f$.

Hier sind die Schaubilder:

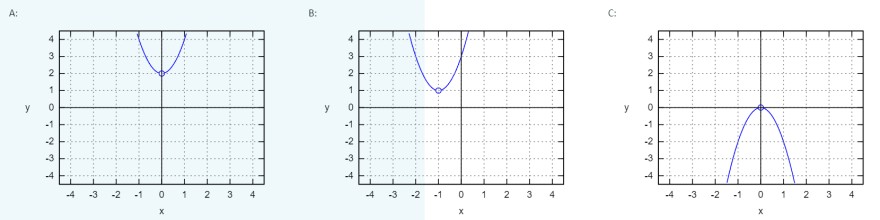
Welches Schaubbild gehört zu der Höhenlinie?
(A, B oder C) $*$

Meine Lösung:

a)

Habe ich 1. Also

$\mathbb{D}_{f}=\left\{(x, y) \in \mathbb{R}^{2} \mid y \neq 1\right.$}

b)

Habe ich 4 - x² - 2x und definionsbreich 1. Also.

Höhenlinie: $y(x)=4 - x² - 2x$ mit $\mathbb{D}_{y}=\mathbb{R} \backslash\{ 1$

c)

Habe ich die Lösung Schaubild C. Da das Schaubild C ist möglich da der Definitionsbereich von f die Punkte (x, y) enthält, an denen y ≥ 1 ist oder

Answer 1

(x² + 2·x + 1)/(y - 1) = 1/2

Auflösen nach

y = 2·(x + 1)² + 1

Das passende Bildchen ist also B.

Comments

Ah mist stimmt habe dann eine mini Frage, Aufgabe a und b sollten dann aber so stimmen und würde bei Aufgabe b) der definitionsbereich 1 auch stimmen denn da war ich mir unsicher

---

Ja. Der Definitionsbereich passt so.