Aufgabe:
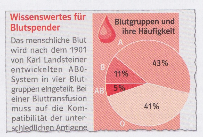
Das untenstehende Kreisdiagramm zeigt die Häufigkeitsverteilung der Blutgruppen in Deutschland. Es werden zufällig 30 Personen, die in Deutschland wohnen, ausgewählt.
(a) Bestimme die Wahrscheinlichkeit, dass mehr als 15 der Personen Blutgruppe A haben.
(b) Bestimme die Wahrscheinlichkeit, dass höchstens fünf der Personen Blutgruppe B oder AB haben.
(c) Bestimme die Wahrscheinlichkeit, dass die Anzahl der Personen mit Blutgruppe 0 um höchstens Sigma vom Erwartungswert abweicht.
(d) Wie viele Personen müsste man zufällig auswählen, um mit einer Wahrscheinlichkeit von mindestens 90% mindestens drei Personen mit der Blutgruppe AB zu bekommen?
Problem/Ansatz:
Kann mir jemand ein erklären, wie man diese Aufgaben rechnet?