Differentialgleichungen erzwungener Schwingung

Question

Aufgabe:

Betrachte für \( \alpha>0 \) wir die erzwungene Schwingung: \( x^{\prime \prime}(t)+\alpha^{2} \cdot x(t)=\cos (\omega \cdot t) \), wobei \( x(0)= \) \( x^{\prime}(0)=0 \).
(a) Löse die Differentialgleichung.
(b) Zeige, dass die Lösung eine Überlagerung von einer „schnellen“ Schwingung (d.h. hohe Frequenz bzw. kleine Periodenlänge) mit einer langsamen Schwingung (d.h. niedrige Frequenz bzw, große Periodenlänge) vorliegt. Ist \( \omega=\alpha \), so ist die Amplitude groß und es tritt Resonanz auf.

Problem/Ansatz:

Wie gehe ich am besten mit dem Lösen einer solchen DGL um?

Und bei (b) habe ich leider überhaupt gar keinen Ansatzpunkt.

Answer 1

Hallo,

zu a )

1. Ansatz x(t)= \( e^{λ t} \)

2 Mal ableiten und x .x', x'' in die DGL einsetzen

2. charakt.Gleichung:

\( α^{2} \) +\( λ^{2} \) =0

λ_1,2= ± iα

\( xh(t)=c_{1} \cos (a t)+c_{2} \sin (a t) \)

3. Ansatz part. Lösung:

\( x_{p}(t)=A \sin (\omega t)+B \cos (\omega t) \)

4.xp 2 Mal ableiten und in die DGL einsetzen, Koeffizientenvergleich

\( x_{p}(t)=\frac{\cos (\omega t)}{a^{2}-\omega^{2}} \)

 5. x= xh+xp

\( x(t)=\frac{\cos (t \omega)}{a^{2}-\omega^{2}}+c_{2} \sin (a t)+c_{1} \cos (a t) \)

 6. Anfangsbedingungen in die Lösung einsetzen:

\( x(t)=\frac{\cos (t \omega)-\cos (a t)}{a^{2}-\omega^{2}} \)

-----------------------------------------------------------------------------------------------------------------

Berechnung part. Lösung:

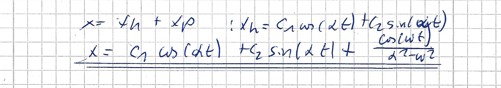
Einsetzen der Anfangsbedingungen:

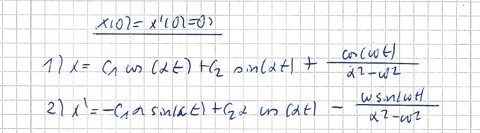
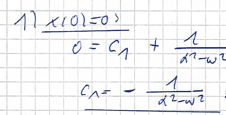
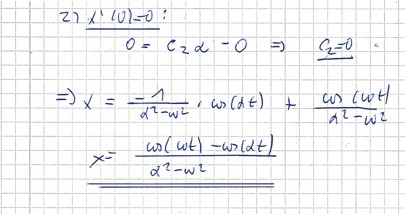
zu b)

Möglicherweise sollst Du das Ganze zeichnen :

https://de.wikipedia.org/wiki/Schwebung

du hast:

y₁= \( \frac{-cos(α t )}{α^{2} - ω^{2}} \)

y₂=\( \frac{cos(ω t )}{α^{2} - ω^{2}} \)

Comments

Danke schonmal!

Aber wie komme ich auf den Ansatz \(x(t)=e^{\lambda t}\)?

---

Das ist der Exponentialansatz vom dem Mathematiker Leonhard Euler.

Es gibt zur Lösung von DGL gewisse Ansätze , siehe Link

Hier Blatt 2, Punkt1

https://micbaum.y0w.de/uploads/LoesungsansaetzeDGLzweiterOrdnung.pdf

Habt Ihr solche DGL nicht behandelt?

---

Danke!

Allerdings bekomme ich als Endlösung folgendes raus:

\(x(t)=\frac{cos(\omega t)-cos(\alpha t)}{\alpha^{2} - \omega^{2}} + \frac {sin(\alpha t)}{\alpha}\)

Ich habe für \(c_{1}\) und \(c_{2}\) folgendes berechnet:

\(c_{1}=\frac{1}{\alpha^{2}-\omega^{2}}\)

\(c_{2}=\frac{1}{\alpha}\)

Ich vermute mal, der Unterschied bei \(c_{2}\) liegt. Mein \(c_{2}\) habe ich aus der Anfangsbedingung \(x^{\prime}(0)=0\) berechnet.

Leider finde ich meinenden Fehler nicht. Wo könnte das Problem bei mir liegen?

---

Und wie gehe ich mit Aufgabenteil (b) um?

Hier habe ich noch weniger Ideen als ich ab (a) hatte.

---

Vielen Dank für die ausführliche Lösung!

Meinen Fehler habe ich gefunden. wir ein einfacher total blöder Umformungsfehler.

Hast du denn auch eine Idee, wie man an (b) herangehen könnte?