\( y=x-\frac{1}{x^{2}} =\frac{x^3-1}{x^2}\)
Definitionsbereich:
alle \(x\) außer \(x=0\) ∈ ℝ
Pole: Nenner ist 0
\(x^2=0\)
\(x=0\)
Bei x= 0 ist \(f(x)\) unstetig
Nullstellen:
\(\frac{x^3-1}{x^2}=0\)
\( x=1 \)
Extrema:
\( y'=\frac{3x^2 \cdot x^2-(x^3-1)\cdot 2x }{x^4}\) mit \(x\) gekürzt :
\( y'=\frac{3x^2 \cdot x-(x^3-1)\cdot 2}{x^3}=\frac{x^3+2}{x^3}\)
\( \frac{x^3+2}{x^3}=0\)
\( x^3=-2\)
\( x^3=-2\)
\(x=-\sqrt[3]{2} ≈-1,3\)
\( y(-\sqrt[3]{2})= \frac{-2-1}{(-\sqrt[3]{2})^{2}}= \frac{-3}{(-\sqrt[3]{2})^{2}}=-\frac{3}{2^{\frac{2}{3}}}≈-1,9\)
Art des Extremwerts:
\( y''(-\frac{3}{2^{\frac{2}{3}}}) =-\frac{6 }{(-\frac{3}{2^{\frac{2}{3}}})^4}<0\) Maximum
Wendepunkte:
\( y''=\frac{3x^2 \cdot x^3 -(x^3+2) \cdot 3x^2}{x^6}\) mit \(x^2\) gekürzt :
\( y''=\frac{3x^2 \cdot x -(x^3+2) \cdot 3}{x^4}=-\frac{6 }{x^4}\)
keine Wendepunkte
Asymptoten mit Polynomdivision
\( (x^3-1):x^2=x \) Rest \(-1\)
\( -(x^3 )\)
__________________
\(-1\)
Somit ist \(y=x\) die Asymptote
Bräuchte Hilfe wie man in Geogebra auf die jeweiligen Werte kommt und die Befehle dazu
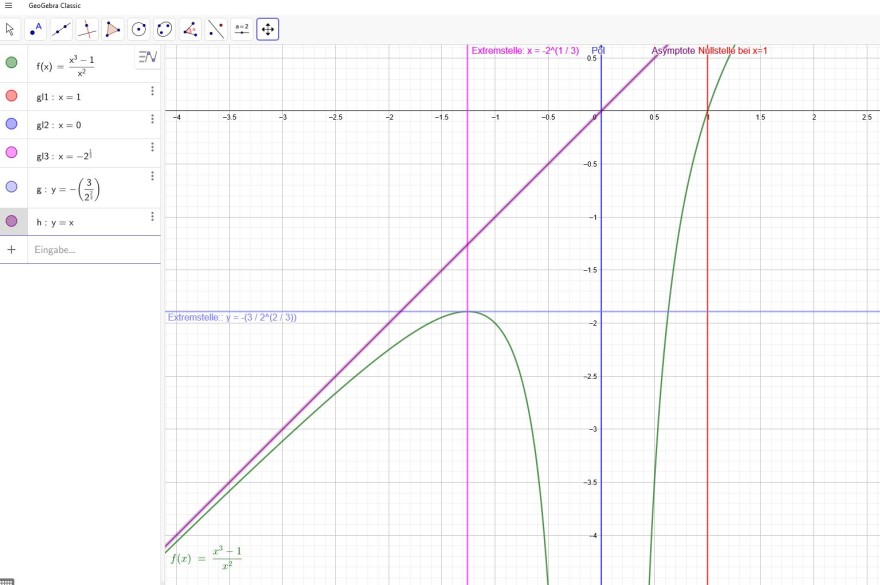
Bei den 3 Punkten übereinander kannst du die Einstellungen aufrufen.
Symmetrie gebrochen-rationaler Funktionen:
https://www.geogebra.org/m/pmRAnJuy