Logarithmische Gleichung lösen, Fehlersuche

Question

Aufgabe:

Folgende Gleichung soll gelöst werden. Wo liegt mein Fehler?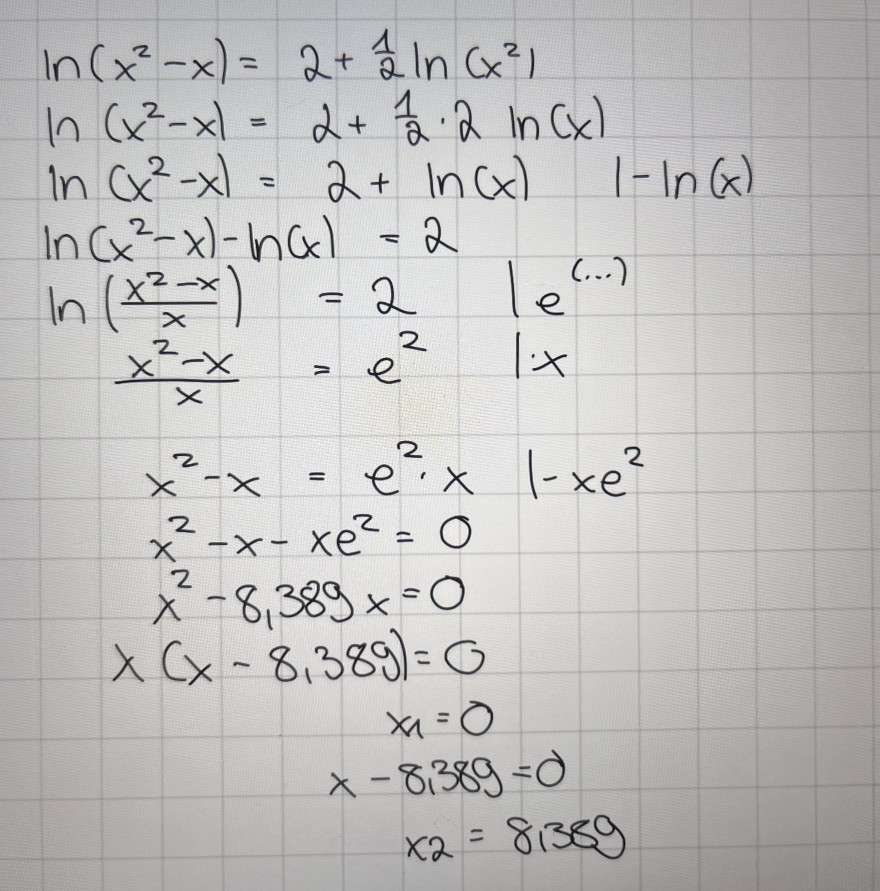

Text erkannt:

\( \begin{array}{l}\ln \left(x^{2}-x\right)=2+\frac{1}{2} \ln \left(x^{2}\right) \\ \ln \left(x^{2}-x\right)=2+\frac{1}{2} \cdot 2 \ln (x) \\ \ln \left(x^{2}-x\right)=2+\ln (x) \quad \mid-\ln (x) \\ \ln \left(x^{2}-x\right)-\ln (x)=2 \\ \left.\ln \left(\frac{x^{2}-x}{x}\right)=2 \quad \right\rvert\, e^{(\ldots)} \\ \left.\frac{x^{2}-x}{x}=e^{2} \quad \right\rvert\, \cdot x \\ x^{2}-x=e^{2} \cdot x \quad \mid-x e^{2} \\ x^{2}-x-x e^{2}=0 \\ x^{2}-8,389 x=0 \\ x(x-8,389)=0 \\ x_{1}=0 \\ x-8,389=0 \\ x_{2}=8,389\end{array} \)

Answer 1

\(x=0\) gehört nicht zum Defbereich der Gleichung.

Und 8.389 ist keine sinnvolle Angabe einer Lösung (\(1+e^2\) dagegen wäre es).

Am einfachsten wäre es, wenn Du sehen würdest, dass man bei \(\frac{x^2-x}x\) das \(x\) kürzen kann. Dann schleppst Du Dir auch nicht die falsche Lösung \(x=0\) rein.

Comments

Ich habe tatsächlich gesehen, dass man x in dem Bruch kürzen kann, allerdings würde da doch dann stehen x-x=e^2 oder?

---

Nein, \(x^2-x=x(x-1)\).

---

Ahhh okay verstehe. Aber mir ist noch nicht ganz klar wieso mein Kürzungsweg nicht klappt. Denn eigentlich ist x^2 ja ein Produkt aus x•x. Könnte ich da nicht einfach ein x rauskürzen?

---

Du kennst doch den Spruch "durch die Summen kürzen nur die D..."?

Deine Umformung auf der rechten Seite geht nur für \(x>0\). Daher findest Du auch nur die positive Lösung. Es gibt aber noch eine negative Lösung.

Damit die Gleichung definiert ist, muss \(x^2-x>0\) sein, also \(x>1\) (den Fall hast Du erledigt) oder \(x<0\). In letzterem Fall ist auf der rechten Seite \(\ln x^2=2\ln (-x)\). Das führt auf \(\frac{x^2-x}{-x}=e^2\) also auf \(x=1-e^2\). Eine weitere Lösung der Gleichung.

---

Den letzten Fall versteh ich irgendwie nicht so ganz.

---

Was genau verstehst Du nicht? Die log-Regeln gelten nur für positive \(x\). Im Fall \(x<0\) ist also \(\ln x^2 = \ln (-x)^2=2\ln (-x)\).