Aufgabe:
21. Ein Glücksrad besteht aus fünf unterschiedlich
großen Sektoren, die mit 0€, 4€,8€, 12€ und 16€
beschriftet sind. Für das einmalige Drehen des
Glücksrades beschreibt die Zufallsgröße X die Auszahlung in €. Siehe Anhang. Das einmalige Drehen des
Glücksrades ist bei einem Einsatz von 7 € fair.
a) Bestimmen Sie die Wahrscheinlichkeiten P(X = 0) und P(X= 16).
b) Beim zweimaligen Drehen wird der höhere der beiden gedrehten Beträge ausgezahlt.
Bestimmen Sie einen fairen Einsatz für dieses Glücksspiel.
Problem/Ansatz:
Ich habe zwei gleichungen aufgestellt aber wie verfahre ich mit den 0 Euro beim erwartunsgwert? Sie machen das c ja quasi irlevant? Wie kann ich das umgehen?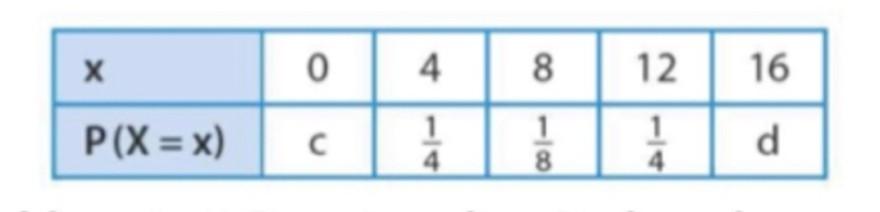
Text erkannt:
\begin{tabular}{|l|c|c|c|c|c|}
\hline \( \mathbf{X} \) & 0 & 4 & 8 & 12 & 16 \\
\hline \( \mathbf{P}(\mathbf{X}=\mathbf{x}) \) & \( \mathrm{C} \) & \( \frac{1}{4} \) & \( \frac{1}{8} \) & \( \frac{1}{4} \) & \( \mathrm{~d} \) \\
\hline
\end{tabular}