(1+x)n ≤ 1+(2n−1)x per Induktion zeigen

Question

Hallöchen,

Ich habe folgende Ungleichung per Induktion zu beweisen: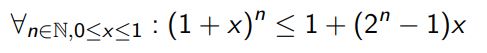

Mein einziges Problem liegt im Induktionsschritt. Ich schaffe da die korrekte Umformung bzw. Abschätzung nicht. Ich kam bisher bis zu diesem Punkt:

$(1+x)^{n+1} \\=(1+x)^{n}*(1+x) \\ \leq (1+(2^{n}-1)x)*(1+x) \leftarrow Induktionsvoraussetzung \\ =(1+(2^{n}x-x))*(1+x) \\ =(1+x)+(2^{n}x-x)*(1+x) \\ =1+x+2^{n}x+2^{n}x^{2}-x-x^{2} \\ =1+2^{n}x+2^{n}x^{2}-x^{2} \\ \leq 1+2^{n}x+2^{n}x-x^{2} \leftarrow da ~ 0\leq x \leq 1 \Longrightarrow x^{2}\leq x \\ =1+2*2^{n}x-x^{2} \\ =1+2^{n+1}x-x^{2}$

Ich habe zuerst gedacht ich könnte -x²<= -x abschätzen und das x ausklammern aber das wäre falsch gewesen, daher hänge ich hier fest. Für Anregungen wäre ich dankbar :)

Text erkannt:

$\forall_{n \in \mathbb{N}, 0 \leq x \leq 1}:(1+x)^{n} \leq 1+\left(2^{n}-1\right) x$

Comments

Meine LaTeX Einbettung hat anscheinend nicht funtioniert. Habe ich mich irgendwo vertan?

Answer 1

$1+2^{n}x+2^{n}x^{2}-x^{2}$ weiter so:

$= 1+2^{n}x+(2^{n}-1)x^{2}$ und wegen x^2 ≤x

$\le 1+2^{n}x+(2^{n}-1)x$

$= 1+(2^{n}+2^{n}-1)x$

$= 1+(2^{n+1}-1)x$

Answer 2

Achte auf das Ziel: Du willst auf die Form $1+x\cdot(...)$ kommen. Mach das erstmal (vor Abschätzungen). Dann schätzt Du in (...) mit $x\le 1$ ab, und dann bist Du fertig.