Könnte mir jemand eine ausführliche Lösung liefern? Wäre sehr dankbar. Mfg
Englisch Version :
At t=0 the influx of a continuous stirred tank reactor war changed from minimal medium to minimal medium + yeast extract. The volume of the liquid phase (V) and the volume flow rate (F) did not change throughout the whole process.
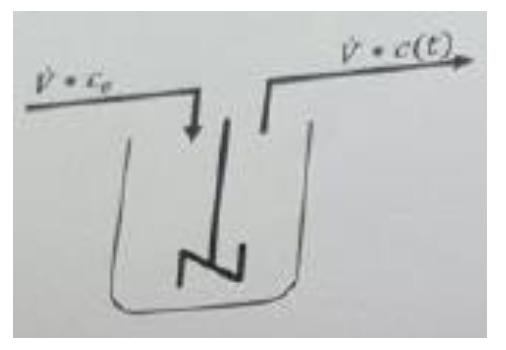
Mass flow = volume flow rate (F) * concentration
ce: concentration of yeast extract in the influx
c(t): Time dependent concentration of yeast extract in the efflux.
The mass balance of yeast extract can be formulated as follows. (V and ce are constants)
(∗())/= F *ce – F * c(t)
a) Differentiate the left side of the equation (V=constant). Use the product rule. If a term cannot besimplified further, write down the differential quotient (e.g. dy(x)/dx). Divide both sides by the flow rate and use τ = V/F to simplify your formula
b) Express the time dt as a multiple of the residence time. Therefore, differentiate θ(t).Next,substitute dt for dθ in the simplified mass balance equation. θ (t) = /τ
c) Solve the resulting differential equation within the range of \int_{0}^{c\theta} d\mathcal{C}(\theta) \quad \text{and} \quad \int_{0}^{\theta} d\mathcal{C}(\theta), respectively.
d) How long does it take to reach a relative yeast extract concentration of 40 % (θ/ce= 0.4). Consider a residence time (τ) of 1 h
Deutsch version :
a) Differenzieren Sie die linke Seite der Gleichung (V = konstant). Verwenden Sie die Produktregel. Falls ein Term nicht weiter vereinfacht werden kann, schreiben Sie den Differentialquotienten auf (z. B. dy(x)/dx). Teilen Sie beide Seiten durch die Flussrate und verwenden Sie τ = V/F, um Ihre Formel zu vereinfachen.
b) Drücken Sie die Zeit dt als Vielfaches der Verweilzeit aus. Differenzieren Sie daher θ(t). Ersetzen Sie anschließend dt durch dθ in der vereinfachten Massenbilanzgleichung. θ(t) = /τ
c) Lösen Sie die resultierende Differentialgleichung im Bereich von \int_{0}^{c\theta} d\mathcal{C}(\theta) \quad \text{und} \quad \int_{0}^{\theta} d\mathcal{C}(\theta), entsprechend.
d) Wie lange dauert es, bis eine relative Hefextraktkonzentration von 40 % (θ/ce= 0.4) erreicht ist? Berücksichtigen Sie eine Verweilzeit (τ) von 1 Stunde.