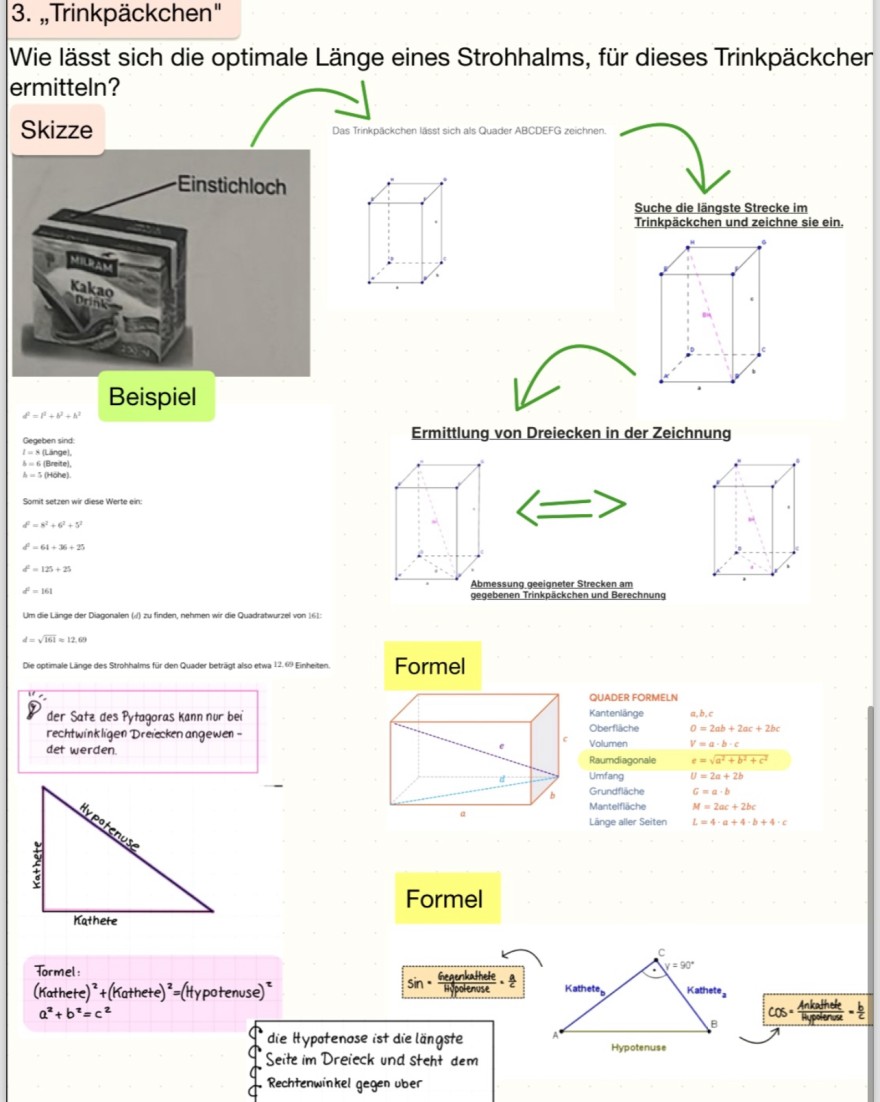
Text erkannt:
3. „Trinkpäckchen"
Wie lässt sich die optimale Länge eines Strohhalms, für dieses Trinkpäckcher ermitteln?
Skizze
Das Trinkpäckchen lässt sich als Quader ABCDEFG zeichnen.
Suche die längste Strecke im Trinkpäckchen und zeichne sie ein.
Beispiel
Gegeben sind:
\( t=s \) (tainge).
is \( =6 \) (Preite),
is \( =5 \) (phohe).
Somit setzen wir diese Werte ein:
\( \begin{array}{l} 4=5^{2}+6^{2}+5^{2} \\ 4=61+35+25 \\ 4^{2}=125+25 \\ 4^{4}=161 \end{array} \)
Um die Lainge der Diagonalen (A) au finden, nehmen wir die Quadratwurzel von i61:
\( 4=\sqrt{161}=12.6 \)
Die optimale Länge des Strohhaims für den Quader beträgt also etwa 12, 6 Einheiten.
der Sate des Pythagoras kann nur bei rechtwinkligen Dreiecken angewen det werden.
Tormel:
(Kathete \( )^{2}+(\text { Kathete })^{2}= \) (Hypotenuse) \( )^{2} \) \( a^{2}+b^{2}=c^{2} \)
Formel
Formel
\( \sin \text { - Gegenkathele } \frac{a}{C} \)
Abmessung.geeigneter Strecken am
QUADER FORMELN Kantenlänge Oberfliche Volumen
\( \text { a. } b, c \)
\( \begin{array}{l} a, b, c \\ 0=2 a b+2 a c+2 b c \\ y=a-b-c \end{array} \)
Raumdiagona
\( e=\sqrt{a^{2}+b^{2}+c^{2}} \)
Umfang Grundhache
\( \begin{array}{c} U=2 a+2 b \\ c=a+b \end{array} \)
Mantelflache
\( M=2 a c+2 b c \) Länge aller Seiten
Kathete
die Hypotenose ist die längste
Seite im Dreieck und steht dem
Hypotenuse
Rechtenwinkel gegen uber
Aufgabe:
Wie lässt sich die optimale Länge eines Strohhalms, für dieses Trinkpäckcher ermitteln?
Problem/Ansatz:
Wie würdet ihr das berechnen? Was ist optimale Länge überhaupt?