Aufgabe:
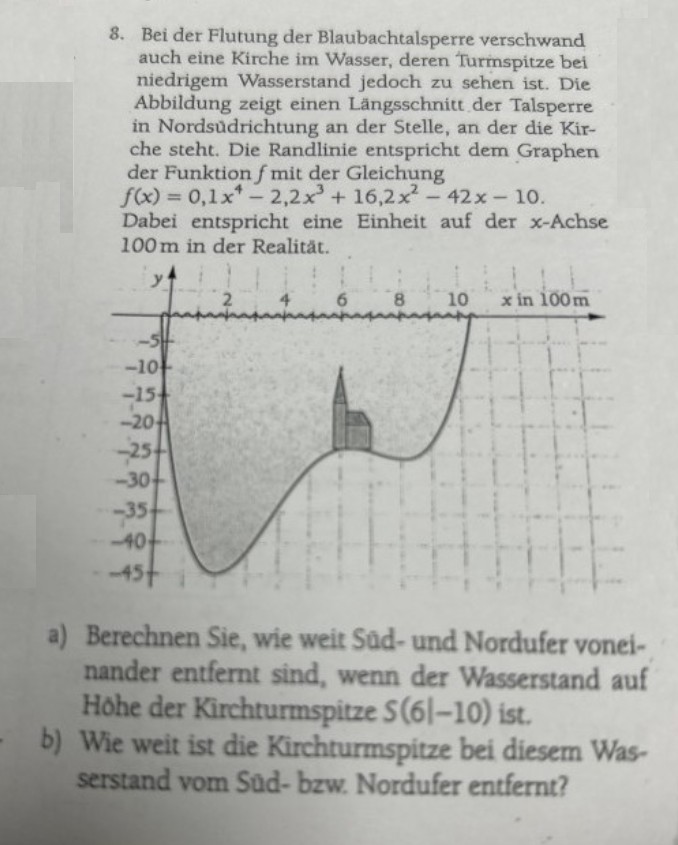
Bei der Flutung der Blaubachtalsperre verschwand auch eine Kirche im Wasser, deren Turmspitze bei niedrigem Wasserstand jedoch zu sehen ist. Die Abbildung zeigt einen Längsschnitt der Talsperre in Nordsudrichtung an der Stelle, an der die Kirche steht. Die Randlinie entspricht dem Graphen der Funktion \( f \) mit der Gleichung
\( f(x)=0,1 x^{4}-2,2 x^{3}+16,2 x^{2}-42 x-10 \text {. } \)
Dabei entspricht eine Einheit auf der \( x \)-Achse \( 100 \mathrm{~m} \) in der Realität.
a) Berechnen Sie, wie weit Süd- und Nordufer voneinander entfernt sind, wenn der Wasserstand auf Hohe der Kirchturmspitze S \( (6 \mid-10) \) ist.
b) Wie weit ist die Kirchturmspitze bei diesem Wasserstand vom Süd- bzw. Nordufer entfernt?
Problem/Ansatz:
Kann jemand mir sagen wie man das berechnet mit dem Blaubachtalspeere