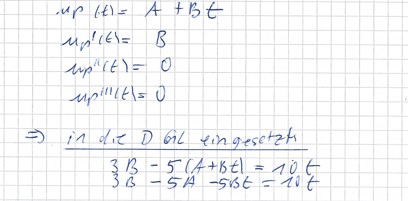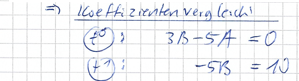Bestimmen Sie eine reelle Darstellung der allgemeinen Lösung der Differentialgleichung

Question

Aufgabe:

a) Bestimmen Sie eine reelle Darstellung der allgemeinen Lösung der Differentialgleichung

$u^{(3)}(t)+u^{\prime \prime}(t)+3 u^{\prime}(t)-5 u(t)=0 .$
b) Bestimmen Sie die allgemeinen Lösungen der Differentialgleichungen:
i) $u^{(3)}(t)+u^{\prime \prime}(t)+3 u^{\prime}(t)-5 u(t)=10$,
ii) $u^{(3)}(t)+u^{\prime \prime}(t)+3 u^{\prime}(t)-5 u(t)=e^{t}$.

Problem:

Leider weiß ich hier nicht weiter

Answer 1

Hallo,

a)

Ansatz:u(t)=e^(λ t)

3 Mal ableiten, in die DGL einsetzen

->Charakt.Gleichung:

λ³ +λ² +3λ-5=0

λ_1,2= -1 ±2i

λ₃=1

-> $u(t)=c_{3} e^{t}+c_{1} e^{-t} \sin (2 t)+c_{2} e^{-t} \cos (2 t)$

zub)

yp 3 Mal ableiten , in die DGL einsetzen, ggf. Koeffizientenvergleich

y=yh+yp

i) wie a, Ansatz yp= A

Begründung: weil die 10 der C_o entspricht (in der Tabelle),hier liegt keine Resonanz vor.

weil in der Störfunktion kein weiterer Term mit t ist , ist er auch nicht länger.

$c_{o}+c_{1} x+c_{2} x^{2}+\ldots+c_{n} x^{n}$

würde 10+20t stehen, lautet der Ansatz C₀+ C1 t

bei: 10+20t +t² dann C₀+ C1 t +C2 t²

ii)wie a, Ansatz yp= A t *e^t

Begründung:

Hier liegt Resonanz vor:

Die Störfunktion lautet e^( 1 · t)

Die 1 ist aber auch eine einfache Lösung der charakt. Gleichung , deswegen mal t

siehe hier:

$c \cdot x \cdot e^{\alpha x}$

Ansätze part. Lösung hier:

https://micbaum.y0w.de/uploads/LoesungsansaetzeDGLzweiterOrdnung.pdf

2.Blatt , Punkt 2

Ich habe die selbe Aufgabenstellung genommen nur aus der 10 eine 10t

Comments

Ich habe eine Frage zu Aufgabe b.

Ich habe die selbe Aufgabenstellung genommen nur aus der 10 eine 10t gemacht um das lösen der Inhomogenität zu üben, nur dabei bin ich auf einen Problem gestoßen und wollte fragen ob der Ansatz so richtig ist und wenn wie das gelöste Gleichungssystem aussieht.

Zu i) hätte ich auch noch eine frage, wir haben den Ansatz yp=A genommen, wie kommt man darauf?

Und woher weiß ich bei ii),dass ich den Ansatz yp= A*t*e^t nehmen muss und nicht A*e^t? (Ich verstehe dort die Begründung der Fälle leider nicht, so wie ich es verstanden habe, geht es hierbei um die Nulstellen Lambda)

Vielen Lieben dank schonmal im vor aus, die Erklärungen sind immer super hilfreich und hilft mir den Stoff gut zu verstehen.

Text erkannt:

14. $402 t$ 10t. $\quad u^{\prime \prime}(t) \neq u^{4}(t)+3 u^{\prime}(t)-5 u(t)=10 t$
$\begin{array}{l} u_{p}=A+A \cdot t \\ u_{p}^{\prime}=A \\ u_{p}^{\prime \prime}=0=u_{p}^{\prime \prime \prime} \end{array}$
$3 A-5 A-5 A \cdot t=10 \cdot t \quad \operatorname{nac} A$
$\rightarrow \text { Din Dal }$

Ansate Blatt2. 2. oberdes.

---

Update: ergänzte Antworten siehe oben

---

Vielen Vielen Dank.

Das hat mir sehr geholfen!