Aufgabe: Funktion maximale Höhe bestimmen
Problem/Ansatz:
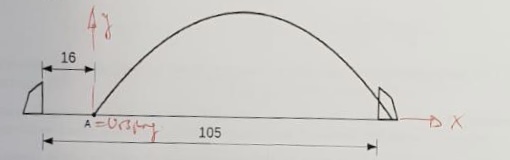
Fußballtraining. Während eines Trainings schießt der Torwart beim Ausschuss den Ball vom Punkt A in Richtung des gegnerischen Tores. A befindet sich am Ende des Strafraumes, 16m von der Torlinie entfernt. Die Flugbahn lässt sich beschreiben durch die Funktion h mit
h(x) = x • tan a - x^2 * (g/2v^2*cos a)
V ... Abschussgeschwindigkeit in m/s, g = 9,81m/s^2 .. Erdbeschleunigung. a ….. Abschusswinkel
X ... horizontale Entfernung (in Meter) von A, h(x) ... Höhe des Balles (in Meter) in der Entfernung x.
Nachstehende Abbildung (nicht maßstabsgetreu) zeigt eine mögliche Flugbahn des als punktförmig angenommenen Balles.
(a) - Begründen Sie mit Hilfe der Differentialrechnung anhand der Funktionsgleichung, dass a (alpha) tatsächlich der Abschusswinkel in A ist.
(b) Der Torwart schießt den Ball mit 30m/s unter 40° ab.
- Ermitteln Sie die maximale Höhe, die der Ball erreicht. [1P]
Ein Fußballtor ist 2, 44m hoch, das Spielfeld ist 105m lang. Ein Tor werde geschossen, wenn der Ball im gegnerischen Tor auf oder hinter der Torlinie aufprallt (vgl. Abbildung).
Überprüfen Sie nachweislich, ob mit diesem Schuss ein Tor erzielt wird. (1P]
Für die Länge s einer Kurve, die Graph einer Funktion f(x) im Intervall [a; b] ist. gilt
S= Integral von a bis b [Wurzel (1 + [f’(x) ] ^2] * dx
-- Berechnen Sie die Länge der Flugbahn des Balles. /1PI
Also ich hätte bei a) f‘ berechen und dann f‘(0) = tan a
Beim Rest habe ich wirklich keine Ahnung