Brennpunkt einer Parabel und Höhe einer Lichtquelle berechnen

Question

Aufgabe:

Eine Terrasse wird von einem nach unten geöffneten Schirm aus reflektierendem Material überspannt, dessen Querschnittslinie einer Parabel entspricht. Ein Punkt am äußeren Rand des Schirms (also auf der Parabel) liegt 80 cm tiefer als der Scheitel der Parabel. Der Durchmesser des Schirms beträgt 400 cm. Konstruieren Sie den Querschnitt in GeoGebra in einem geeigneten Maßstab und ermitteln Sie die Parabelgleichung auch rechnerisch. Wie weit unterhalb des höchsten Punktes bzw. wie weit unterhalb des Scheitels muss eine Lichtquelle montiert sein, damit sie im Brennpunkt der Parabel liegt und so die Lichtstrahlen nach der Reflektion an der Schirmfläche parallel zu Boden strahlen?

Problem/Ansatz:

Soweit habe ich den Querschnitt in Geogebra abgebildet, den Brennpunkt mit der Formel P = (0, 1/(4*a)) berechnet und die Parabel rechnerisch ermittelt. Mein Problem liegt nun beim zweiten Teil der Aufgabe. Ich verstehe nicht genau wie ich da vorgehen soll bzw. was ich überhaupt zeigen soll. Anbei meine Ausarbeitung aus Geogebra zu der Übung:

Answer 1

Mache es umgedreht. Lasse eine Gerade parallel zur y-Achse auf die Parabel auftreffen und konstruiere das Spiegelbild der auftreffenden Gerade (bei Spiegelung am Einfallslot). Der gespiegelte Strahl verläuft durch den Brennpunkt.

(Das Einfallslot steht senkrecht auf der Tangente.)

Comments

Danke für deine Antwort!

Ich habe das jetzt so in Geogebra gemacht, wie du gemeint hast, es sieht dann folgendermaßen aus: Ich verstehe nur nicht genau, wie mir das jetzt weiterhelfen soll, da ich ja die Höhe der Lichtquelle ermitteln soll, was auch immer das heißen mag. Kannst du mir da bitte weiterhelfen?

Vielen Dank!

---

Dein Punkt P ist der Brennpunkt. Er liegt in einem gewissen Abstand unterhalb des Scheitelpunkts. Dieser Abstand ist gesucht.

---

Hallo

du hast die Formel benutzt die den Abstand des Brennpunktes vom Scheitel  bestimmt , P ist also 125 cm unter dem Scheitel nicht bei y=-125cm, da hast du den Brennpunkt ja auch konstruiert und da muss die Lichtquelle hängen.(obwohl das für ne Lampe eigenartig ist)

Gruß lull

Answer 2

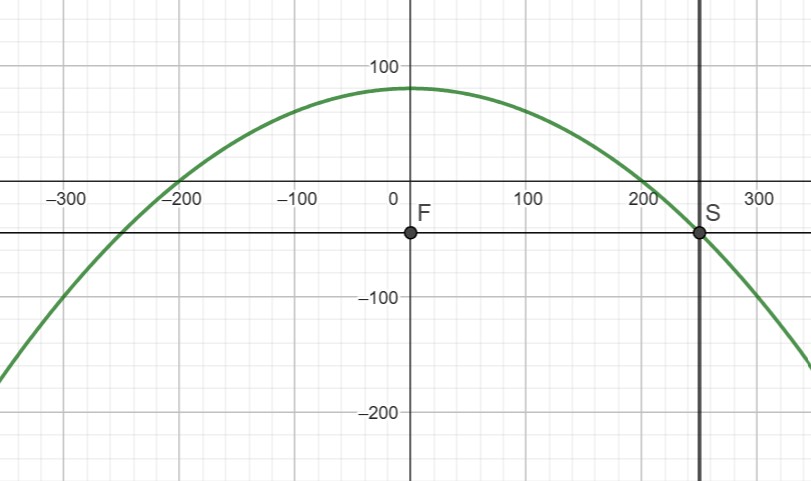
f(x) = 80 - 80/200^2·x^2 = 80 - 0.002·x^2

Der Brennpunkt sollte dann sein bei

B(0 | 80 + 1/(4·(- 0.002))) = B(0 | - 45)

Grundsätzlich kannst du ja fragen. wo die Steigung -1 ist.

f'(x) = - 0.004·x = -1 --> x = 250
f(250) = -45

In dieser Höhe müsste dann eben auch der Brennpunkt sein.