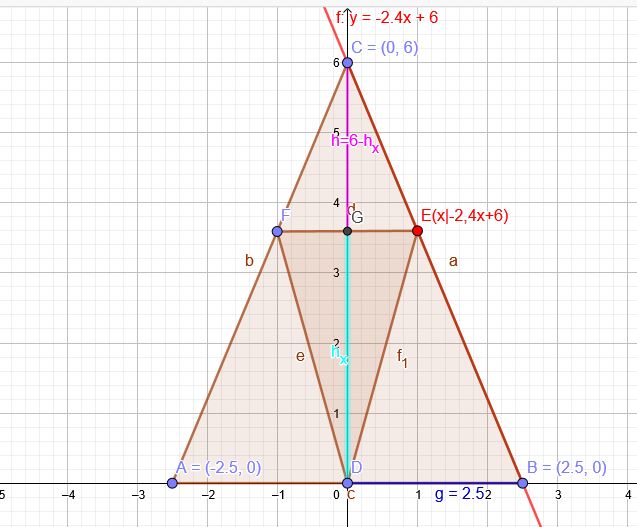
e)
\( \frac{6-h_x}{x}=\frac{6}{2,5} \)
\( 15-2,5h_x =6x\)
\( 2,5h_x =15-6x\)
\(h_x =\frac{15-6x}{2,5}\)
\(h_x =-2,4x+6\)
\(V= \frac{1}{3} \cdot x^{2} \cdot π \cdot (-2,4 x+6) \)
\(V= -\frac{1}{3} \cdot x^{2} \cdot π \cdot (2,4 x-6) \)
\(V= -\frac{1}{3} \cdot x^{2} \cdot π \cdot 2,4 \cdot (x-2,5) \)
\(V= -0,8\cdot x^{2} \cdot π \cdot (x-2,5) \)
f)
\(V(x)= -0,8\cdot x^{2} \cdot π \cdot (x-2,5) \) soll maximal werden.
\(V'(x)= -1,6\cdot x \cdot π \cdot (x-2,5) +( -0,8\cdot x^{2} \cdot π)\cdot 1\)
\( -1,6\cdot x \cdot π \cdot (x-2,5) - 0,8\cdot x^{2} \cdot π=0\)
\( -1,6\cdot x^2 +4 - 0,8\cdot x^{2} =0\)
\(2,4 x^2 =4\)
\( x^2 =\frac{5}{3}\)
\( x =±\sqrt{\frac{5}{3}}\)
\(V=... \)